Le transformer illustré

Cet article est une traduction de The Illustrated Transformer par Jay Alamar.

Dans l’article précédent, on a vu l’attention – une méthode omniprésente dans les modèles modernes de deep learning. L’attention est un concept qui a amélioré la performance des applications de neural machine translation. Dans cet article, on va regarder le transformer – un modèle qui utilise l’attention afin d’augmenter la vitesse avec laquelle ces modèles peuvent être entraînés. Le transformer surpasse le modèle Neural Machine Translation de Google pour des tâches spécifiques. Le bénéfice principale, pourtant, vient de la manière dont le transformer peut être parallelisé. En fait, Google Cloud recommande d’utiliser le transformer comme modèle de référence pour leur produit de Cloud TPU. Alors, essayons de demonter le modèle pour voir comment ça fonctionne.

Le transformer a été proposé dans l’article Attention is All You Need. Une implémentation en TensorFlow est disponible comme partie du package Tensor2Tensor. Le groupe NLP de Harvard a crée une guide annotant le papier avec une implémentation PyTorch. Dans cet article, on va essayer de sur-simplifier les choses un peu et présenter les concepts un à la fois, afin de les rendre plus compréhensibles pour ceux et celles qui n’ont pas une connaissance profonde du sujet.

Une vue plongeante

Commençons en regardant le modèle comme une simple boîte noire. Pour une application de traduction à la machine, il prendrait à l’entrée une phrase dans une langue, et il sortirait sa traduction dans une autre langue.

En ouvrant ce modèle qui rappelle Optimus Prime, on voit un composant d’encodage, un composant de décodage, et les connexions entre les deux.

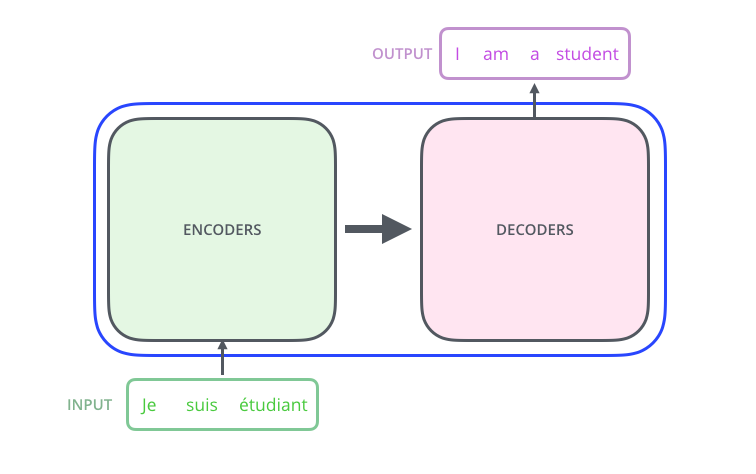
Le composant d’encodage est une pile d’encodeurs (l’article en empile six – il n’y a rien de magique à propos du numéro six; on peut absolument expérimenter avec des autres arrangements). Le composant de décodage est une pile de décodeurs du même numéro.

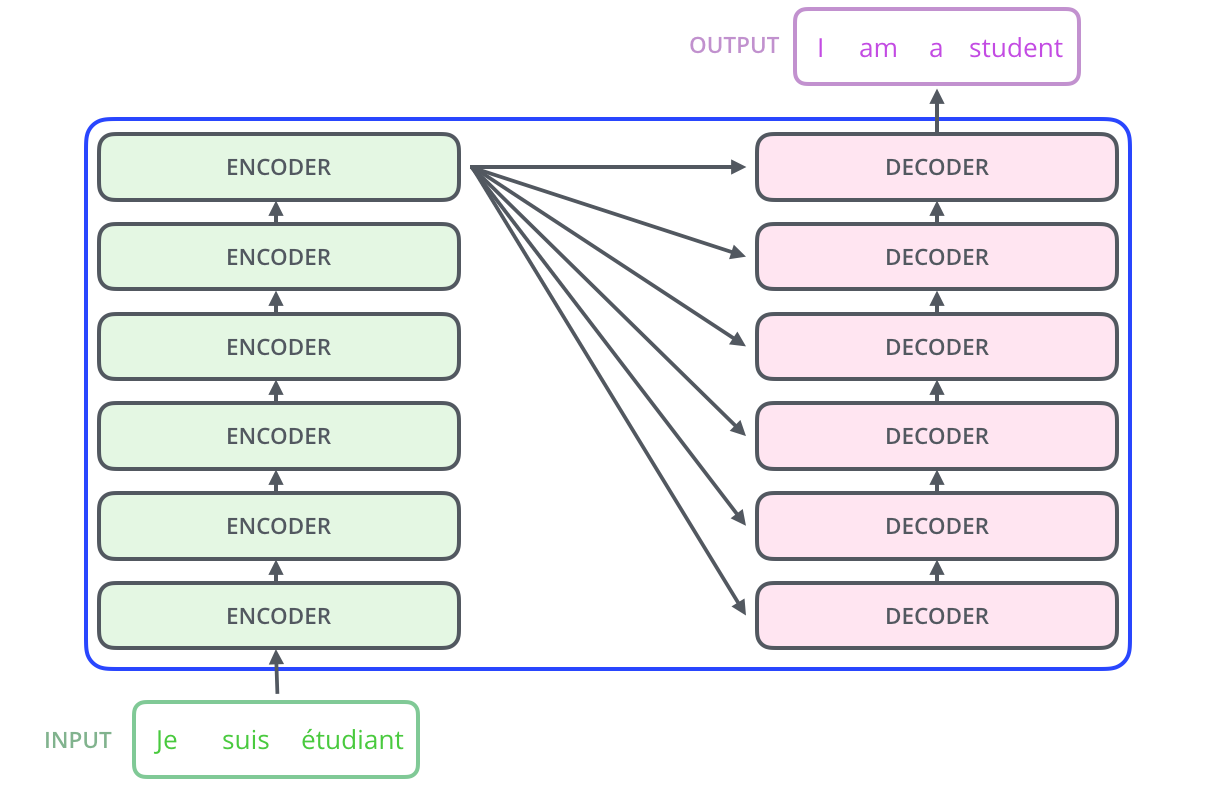
Les encodeurs sont tous idéntiques en structure (mais ils ne partagent pas de poids). Chaque encodeur comprend deux sous-couches:

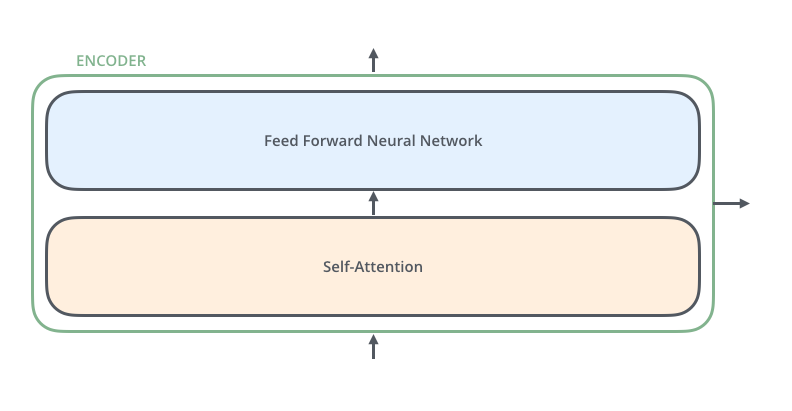
Les données à l’entrée de l’encodeur coulent d’abord dans une couche de self-attention – c’est une couche qui aide l’encodeur à regarder les autres mots de la phrase d’entrée au fur et à mésure qu’il encode un mot spécifique. On examinera la couche self-attention de plus près plus tard.

Les données de sortie de la couche self-attention sont dirigées ensuite à un réseau neuronale feed-forward. C’est ce même réseau feed-forward qui va s’appliquer independamment à chaque position.

Le décodeur a ces deux couches, mais entre elles, il y a une couche d’attention qui aide le décodeur à se concentrer sur les parties pertinentes de la phrase d’entrée (l’attention fait quelque chose de similaire dans les modèles seq2seq.)

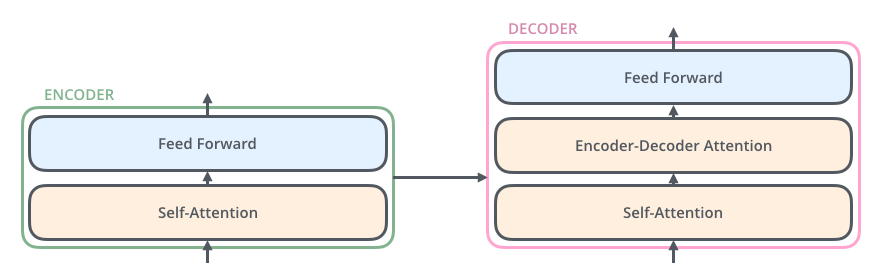
Rajoutons les tenseurs

Maintenant que l’on a vu les composants majeurs du modèle, regardons les multiples vecteurs et tenseurs et la manière dont ils coulent entre ces composants, afin de transformer les données à l’entrée d’un modèle entraîné en des données de sortie.

Comme on fait habituellement pour les applications en NLP, on commence par transformer chaque mot à l’entrée en vecteur via un algorithme d’embedding.

Chaque mot a un embedding, un vecteur de taille 512. On va représenter ces vecteurs avec ces boîtes simples.

Le processus d’embedding n’arrive que dans l’encodeur le plus bas. L’abstraction commune de tous les encodeurs, c’est qu’ils reçoivent tous une liste de vecteurs, chacun de taille 512. Dans l’encodeur le plus bas, cette liste est les embeddings, mais dans les autres encodeurs, c’est la sortie de l’encodeur précédent. On peut changer la taille de cette liste comme hyperparamètre. En gros, ce serait la longueur de la phrase la plus longue dans nos données d’entraînement.

Après que l’on fait les embeddings de nos mots à l’entrée, chaque embedding coule dans les deux couches de l’encodeur.

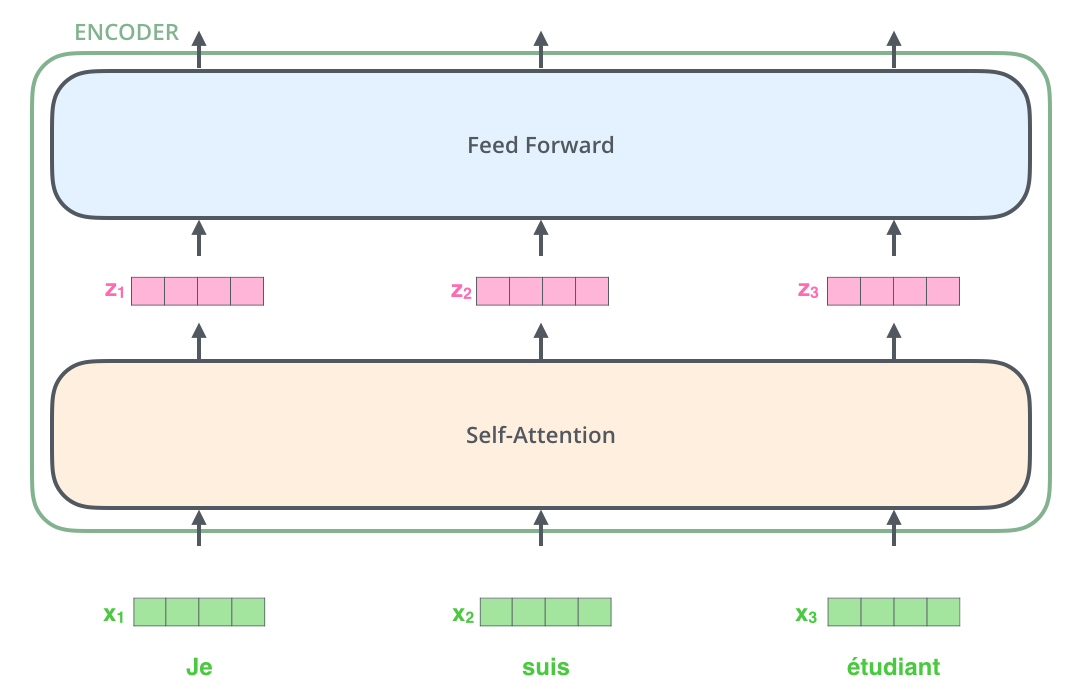
Ici on commence à voir une propriété clé du transformer: le mot à chaque position coule dans son propre chemin dans l’encodeur. Il y a des dépendances entre ces chemins dans la couche self-attention. La couche feed-forward n’a pas ces dépendences, pourtant, et donc ces multiples chemins peuvent être exécutés en parallèle pendant qu’ils coulent dans la couche feed-forward.

Ensuite, on va échanger notre exemple pour une exemple plus court, et on verra ce qui arrive dans chaque sous-couche de l’encodeur.

Là on encode!

Comme on a déjà dit, un encodeur reçoit une liste de vecteurs à l’entrée. Il traite cette liste en passant ces vecteurs à une couche self-attention, puis à un réseau feed-forward, et finalement il envoit les données de sortie en haut, au prochain encodeur.

Le mot à chaque position passe dans un processus de self-attention. Ensuite, ils passent chacun dans un réseau feed-forward – exactement le même réseau pour chaque vecteur, qui y coulent séparément.

Self-attention d’un haut niveau

Ne vous laissez pas duper à croire que tout le monde sait déjà c’est quoi, le self-attention. Personellement, je n’avais jamais vu le concept avant de lire l’article Attention is All You Need. Voyons comment ça marche.

Disons que la phrase suivante est une phrase d’entrée qu’on aimerait traduire:

The animal didn't cross the street because it was too tired

ou en français,

L'animal n'a pas traversé le boulevard parce qu'il était trop fatigué

À quoi it (ou il) se réfère-t-il? Cela se réfère-t-il au boulevard (street) ou à l’animal (animal)? C’est une question simple pour un être humain, mais une question difficile pour un algorithme.

Quand le modèle traite le mot it (ou il), la self-attention permet une association entre it (ou il) et animal.

Au fur et à mesure que le modèle traite chaque mot (à chaque position dans la phrase d’entrée), la self-attention lui permet de regarder des autres positions dans la phrase d’entrée qui peuvent mener à un meilleur encodage pour ce mot.

Si vous connaissez les RNN (recurrent neural network), envisagez comment son entretien d’un état caché permet à un RNN d’incorporer sa représentation des mots/vecteurs précédents déjà traités avec le mot/vecteur qu’il traite actuellement. Self-attention est la méthode du transformer qui intégre la “compréhension” des autres mots pertinents dans le traitement du mot actuel.

Pendant que l’on encode le mot it dans l’encodeur #5 (l’encoder le plus haut dans la pile), une partie du mécanisme d’attention se concentrait sur the animal, et a integré une partie de sa représentation dans l’encodage de it.

Jetez un coup d’œil au notebook Tensor2Tensor où l’on peut télécharger un modèle transformer et l’examiner via une visualisation interactive.

Self-attention en détail

Regardons d’abord comment calculer la self-attention avec des vecteurs, et ensuite comment l’implémenter en vrai – avec des matrices.

La première étape dans le calcul de la self-attention, c’est créer trois vecteurs de chaque vecteur d’entrée de l’encodeur (en ce cas, c’est l’embedding de chaque mot). Pour chaque mot, on crée un vecteur Query, un vecteur Key, et un vecteur Value. Ces vecteurs sont crées en multipliant l’embedding par trois matrices que l’on a déjà entraîné.

Ces nouveaux vecteurs sont plus petits en dimension que le vecteur d’embedding. Leur dimensionalité est 64, tandis que les vecteurs d’entrée/sortie ainsi que les vecteurs d’embedding ont une dimensionalité de 512. Ce n’est pas nécessaire qu’ils soient plus petits; ceci est un choix d’architecture pour rendre le calcul de la multiheaded attention constante (pour la plupart).

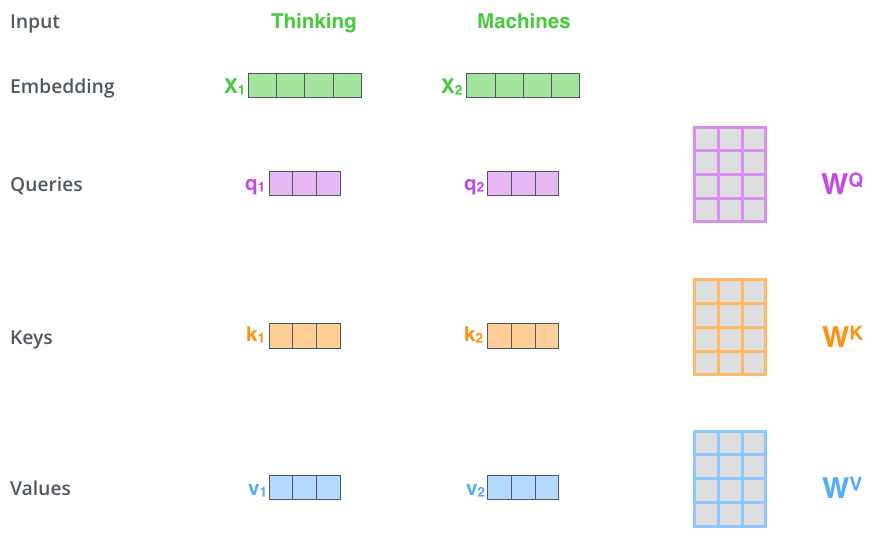La multiplication de $x_{1}$ par la matrice de poids $WQ$ produit $q_{1}$, le vecteur Query qui s’associe avec ce mot. On finit par créer des projections Query, Key, et Value pour chaque mot dans la phrase d’entrée.

Quels sont les vecteurs Query, Key, et Value?

Ils sont des abstractions qui sont utiles pour le calcul et la compréhension de l’attention. Après avoir lu à propos du calcul, vous allez savoir tout ce qui est nécessaire pour comprendre le rôle que chaque vecteur joue.

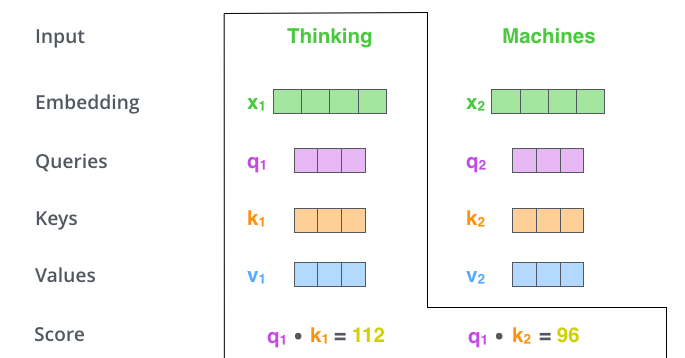
La deuxième étape dans le calcul de la self-attention. Disons que l’on fait le calcul de la self-attention pour la première mot dans cet exemple, Thinking. Il faut donner un score à chaque mot de la phrase d’entrée, comparé à ce mot. Ce score détermine combien de concentration à mettre sur des autres parties de la phrase d’entrée pendant que l’on encode un mot à une certaine position.

Ce score se calcule en prenant le produit scalaire du vecteur Query et le vecteur Key du mot que l’on encode. Si on traite la self-attention pour la mot à position #1, le premier score serait le produit scalaire de $q_{1}$ et $k_{1}$. Le deuxième score serait le produit scalaire de et $q_{1}$ et $k_{2}$.

Les troisième et quatrième étapes sont de diviser les scores par 8 (la racine carrée de la dimension des vecteurs Key dans l’article – 64. Cette stratégie mène aux gradients plus stables. On pourrait avoir des autres valeurs ici, mais ceci est le défaut), ensuite de passer le resultat dans une opération softmax. Le softmax normalise les scores pour qu’ils soient tous positifs et qu’ils se somment à 1.

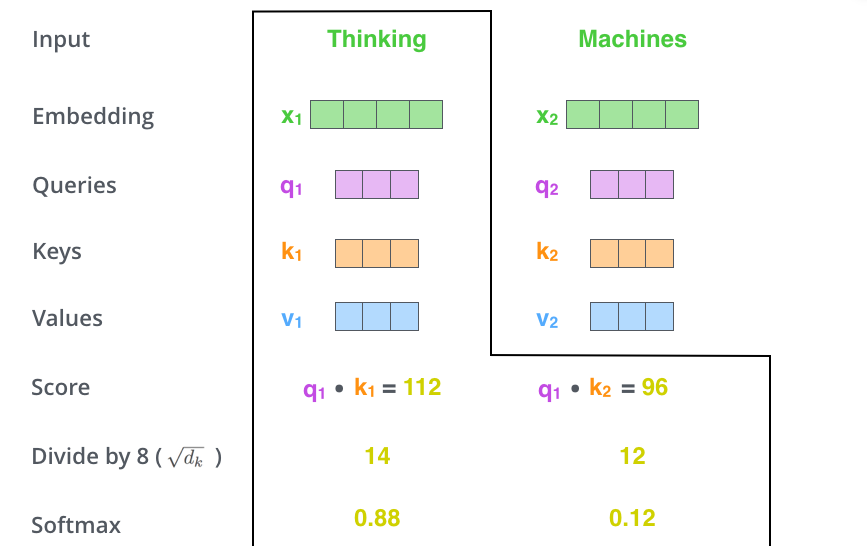
Ce score softmax détermine combien que chaque mot va être exprimé à cette position. Clairement, le mot à cette position va avoir le score softmax le plus haut, mais quelquefois il est utile de faire attention à un autre mot qui est pertinent au mot actuel.

La cinquième étape est de multiplier chaque vecteur Value par le score softmax (en préparation de les sommer). L’intuition ici est de garder intacts les valeurs des mots sur lesquels on veut se concentrer, et de noyer les mots sans rapport (en les multipliant par des petits chiffres comme 0.001, par exemple).

La sixième étape est de sommer les vecteurs Value pondérés. Ceci produit la sortie de la couche self-attention à cette position (pour le premier mot).

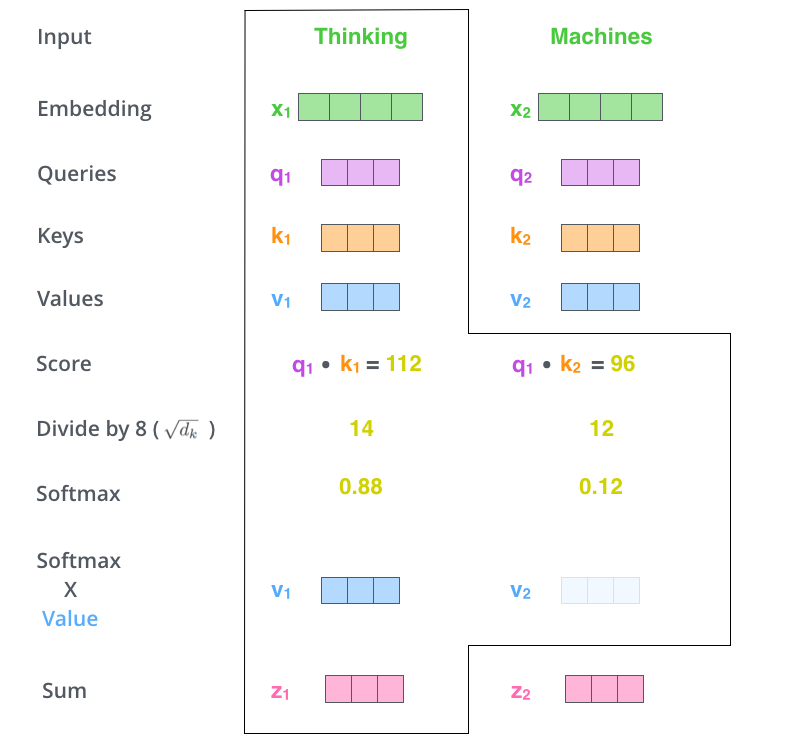
Ceci conclut le calcul de la self-attention. Le vecteur résultant est un vecteur que l’on peut envoyer au réseau feed-forward. Dans la vraie implémentation, pourtant, ce calcul se fait en forme matricielle pour un traitement plus rapide. Regardons comment ça fonctionne, maintenant que l’on a vu l’intuition du calcul sur le niveau de mot.

Calcul matriciel de la self-attention

La première étape est de calculer les matrices Query, Key, et Value. On fait ça en emballant nos embeddings dans une matrice $X$, et la multipliant par les matrices de poids que l’on a entraîné ($W^{Q}$, $W^{K}$, et $W^{V}$).

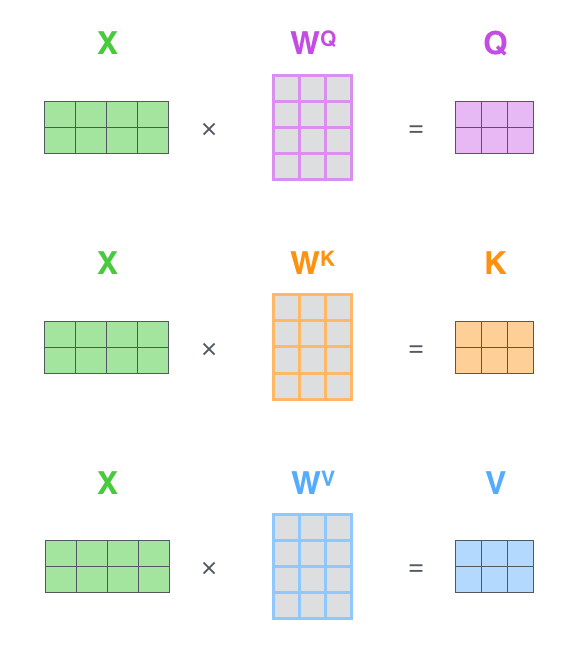Chaque rangée dans la matrice correspond à un mot dans la phrase d’entrée. On voit encore la différence de taille du vecteur embedding (512, ou 4 carrés dans la figure), et les vecteurs $q$/$k$/$v$ (64, ou 3 carrés dans la figure).

Au final, vu que l’on travaille avec des matrices, on peut combiner les étapes deux jusqu’à six dans une formule pour le calcul de la sortie de la couche self-attention.

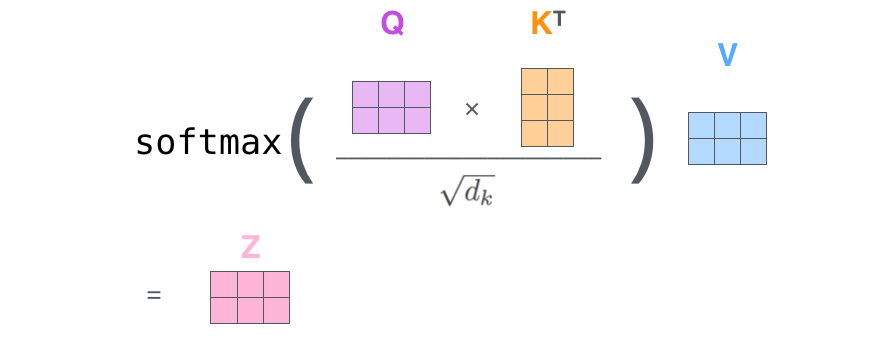Le calcul de la self-attention en forme matricielle.

La bête aux multiples têtes

L’article a raffiné la couche self-attention en rajoutant un mécanisme qui s’appelle multi-headed attention (l’attention aux multiples têtes). Ce mécanisme améliore la performance de la couche d’attention de deux façons:

Il étend la capacité du modèle de se concentrer sur des multiples positions. Oui, dans l’exemple précédent, $z_{1}$ contient un peu de chaque autre encodage, mais il pourrait être dominé par le mot actuel en soi. Ce serait utile si on traduit une phrase comme l’animal n’a pas traversé le boulevard parce qu’il était trop fatigué, on aimerait savoir à quel mot il se réfère.
Il donne à la couche d’attention des multiples “sous-espaces de représentation”. Comme on va voir prochainement, quand on utilise la multi-headed attention, on a plusieurs ensembles de matrices de poids Query/Key/Value (le transformer utilise huit têtes d’attention, alors on finit avec huit ensembles pour chaque encodeur/décodeur). Chaque ensemble s’initialise de manière aléatoire. Ensuite, après l’entraînement, chaque ensemble s’utilise pour faire une projection des embeddings à l’entrée (ou des vecteurs des encodeurs/décodeurs plus bas) dans une autre sous-espace de représentation.

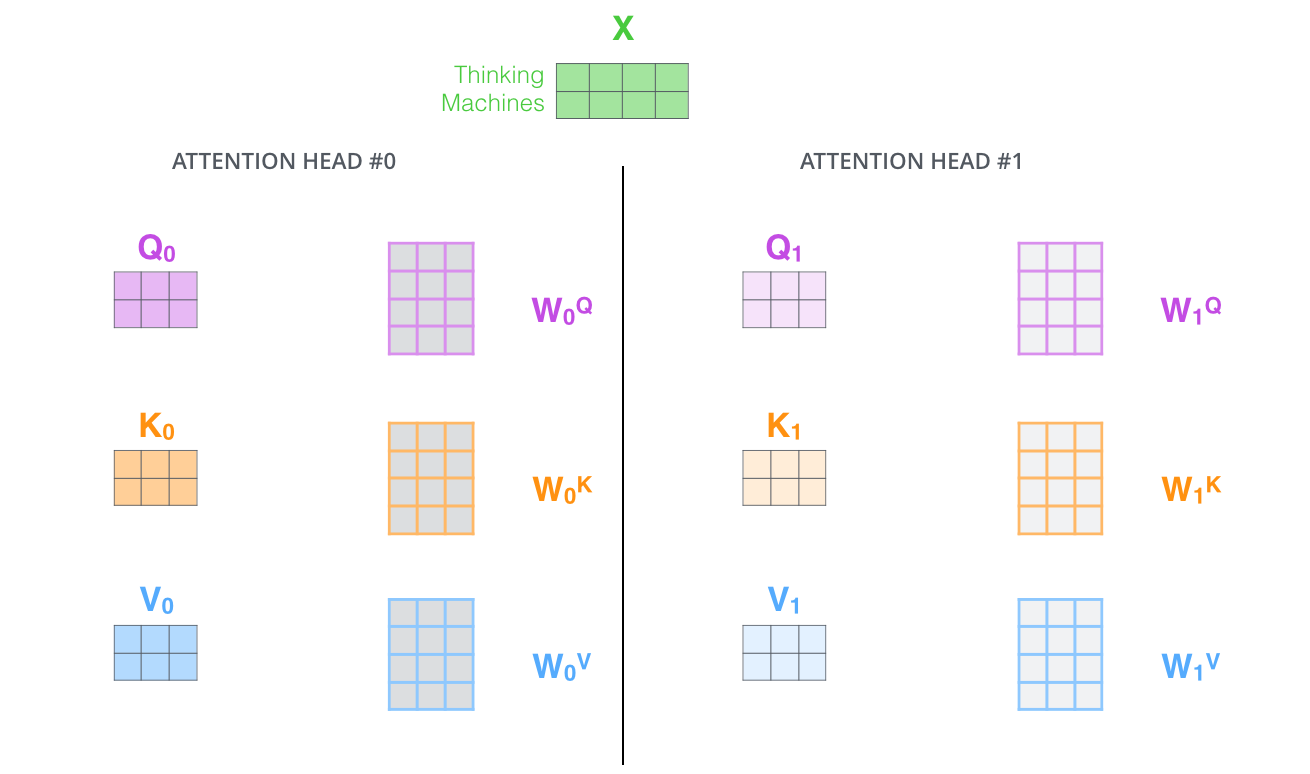Avec la multi-headed attention, on maintient plusieurs matrices de poids $W^{Q}$/$W^{K}$/$W^{V}$ pour chaque tête, donnant des différentes matrices $Q$/$K$/$V$ comme résultat. Comme avant, on multiplie $X$ par les matrices $W^{Q}$/$W^{K}$/$W^{V}$ pour produire les matrices $Q$/$K$/$V$.

Si l’on fait le même calcul de self-attention que l’on vient d’expliquer, huit fois différentes avec des différentes matrices de poids, on finit avec huit matrices $Z$ différentes.

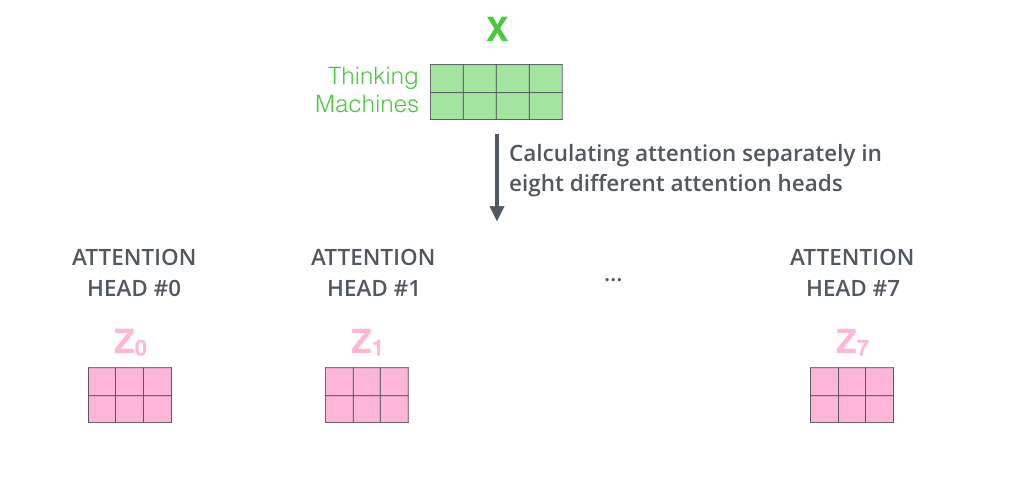
Cela nous laisse avec un défi. La couche feed-forward ne s’attend pas à huit matrices – elle s’attend à une seule matrice (un vecteur pour chaque mot). Il nous faut une façon de combiner ces huites matrices en une matrice.

Comment peut-on faire ça? On concatène les matrices, puis on les multiplient par une matrice de poids supplementaire, $W^{O}$.

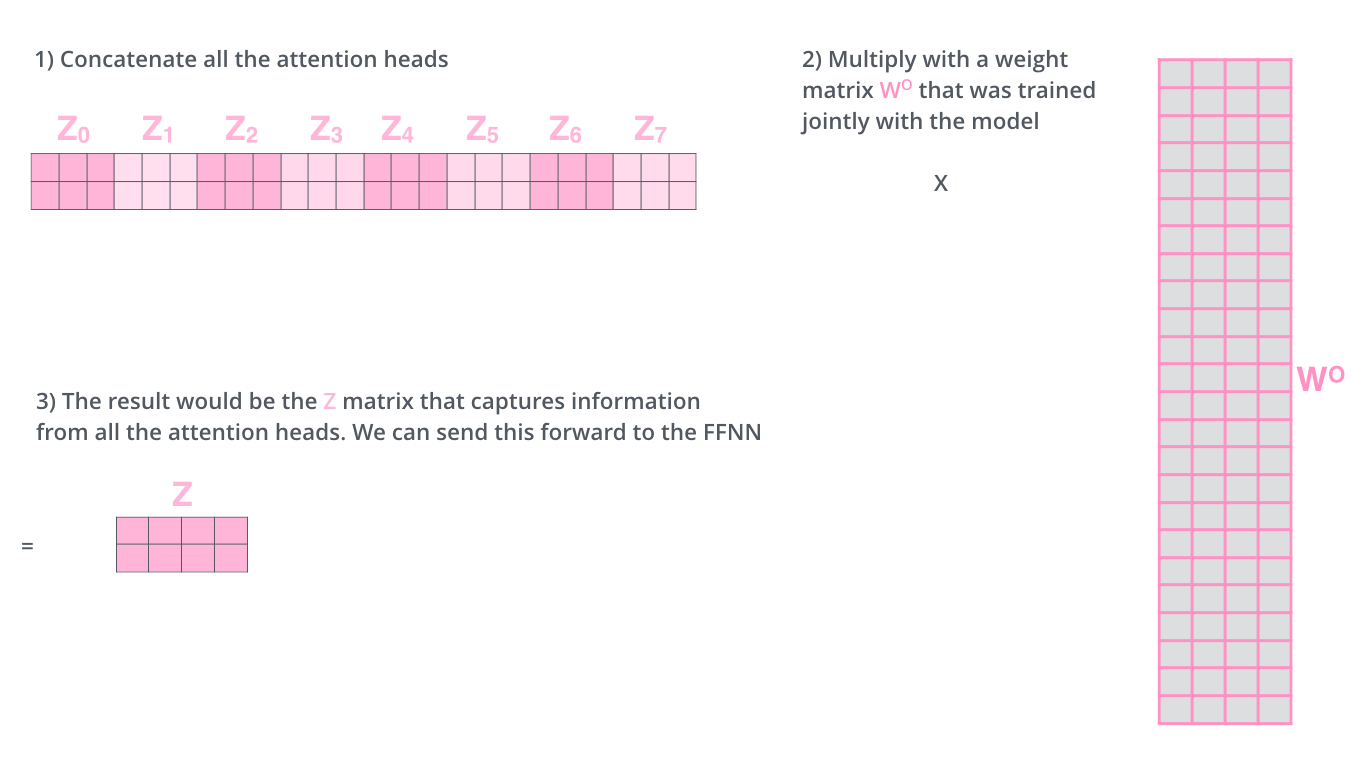
C’est pas mal tout pour le calcul de multi-headed attention. Je me rends compte que c’est beaucoup de matrices. J’essaie de les mettre toutes dans une figure pour que l’on puisse tout voir à la fois:

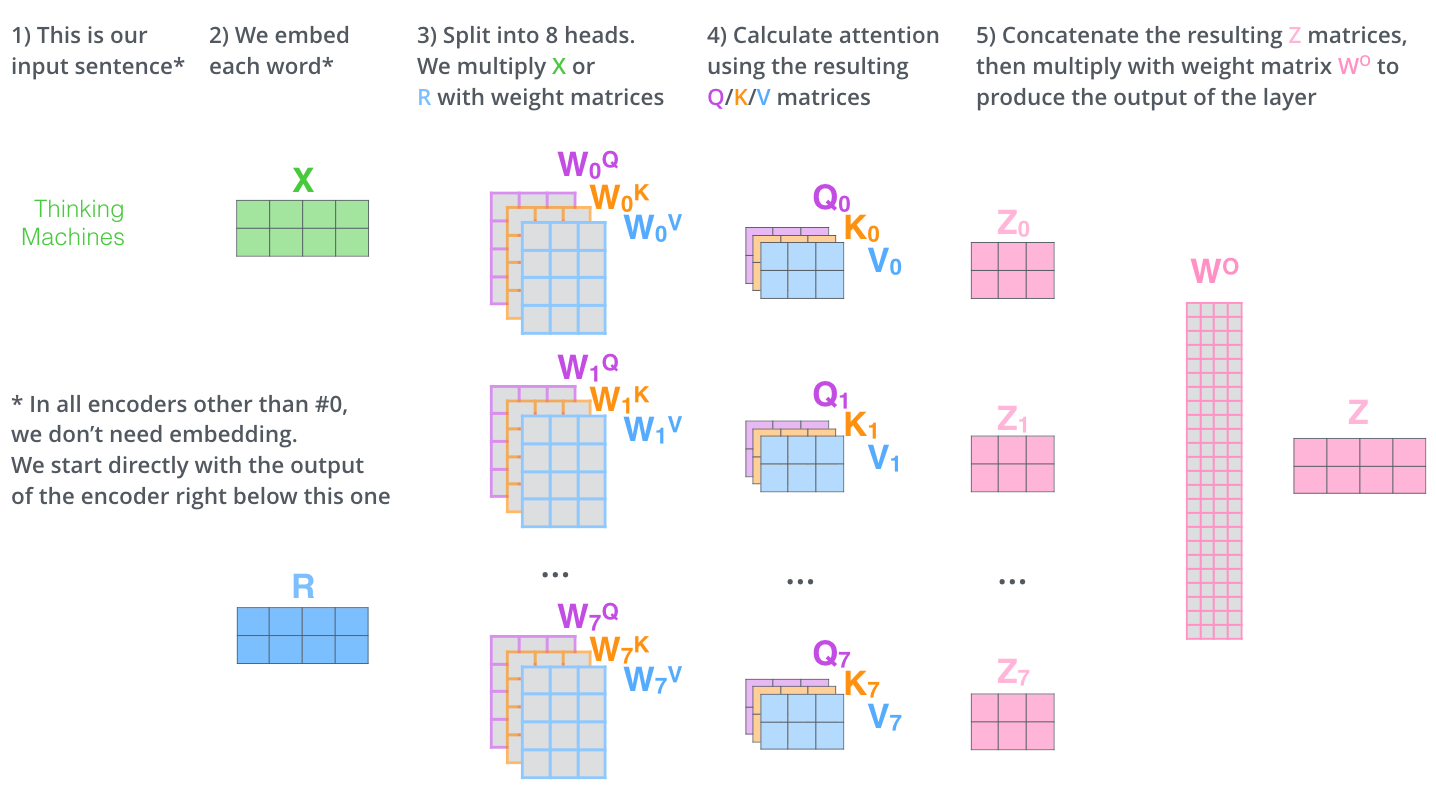
Maintenant que l’on a expliqué les multiples têtes d’attention, regarderons de nouveau notre exemple précédent pour voir où les différentes têtes d’attention se concentrent, pendant que l’on encode le mot it (ou il) dans notre phrase:

Pendant que l’on encode le mot it, une tête d’attention se concentre le plus sur the animal, tandis qu’une autre tête se concentre sur tired – d’une certaine façon, la représentation du modèle du mot it intègre une partie de la représentation de animal et de tired.

Si on rajoute toutes les têtes d’attention à l’image, pourtant, les choses deviennent plus difficiles à interpréter:

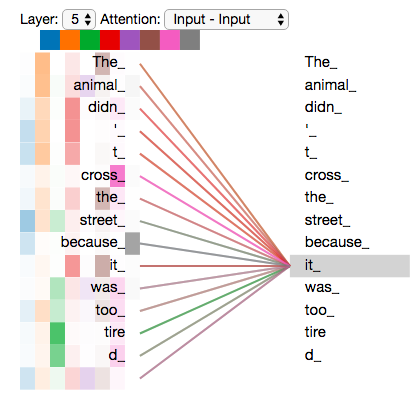
Représenter l’ordre de la séquence avec des encodages positionnels

Une chose qui manque du modèle selon notre explication actuelle, c’est une façon de prendre l’ordre des mots de la phrase d’entrée en compte.

Pour s’adresser à ça, le transformer rajoute un vecteur à chaque embedding d’entrée. Ces vecteurs suivent un motif spécifique que le modèle apprend, ce qui aide le modèle à determiner la position de chaque mot, ou la distance entre des mots différents de la séquence. L’intuition ici est que rajouter ces valeurs aux embeddings fournit des distances significatives entre les vecteurs embedding, une fois qu’ils sont projetté dans les vecteurs $Q$/$K$/$V$, et pendant l’attention de produit scalaire.

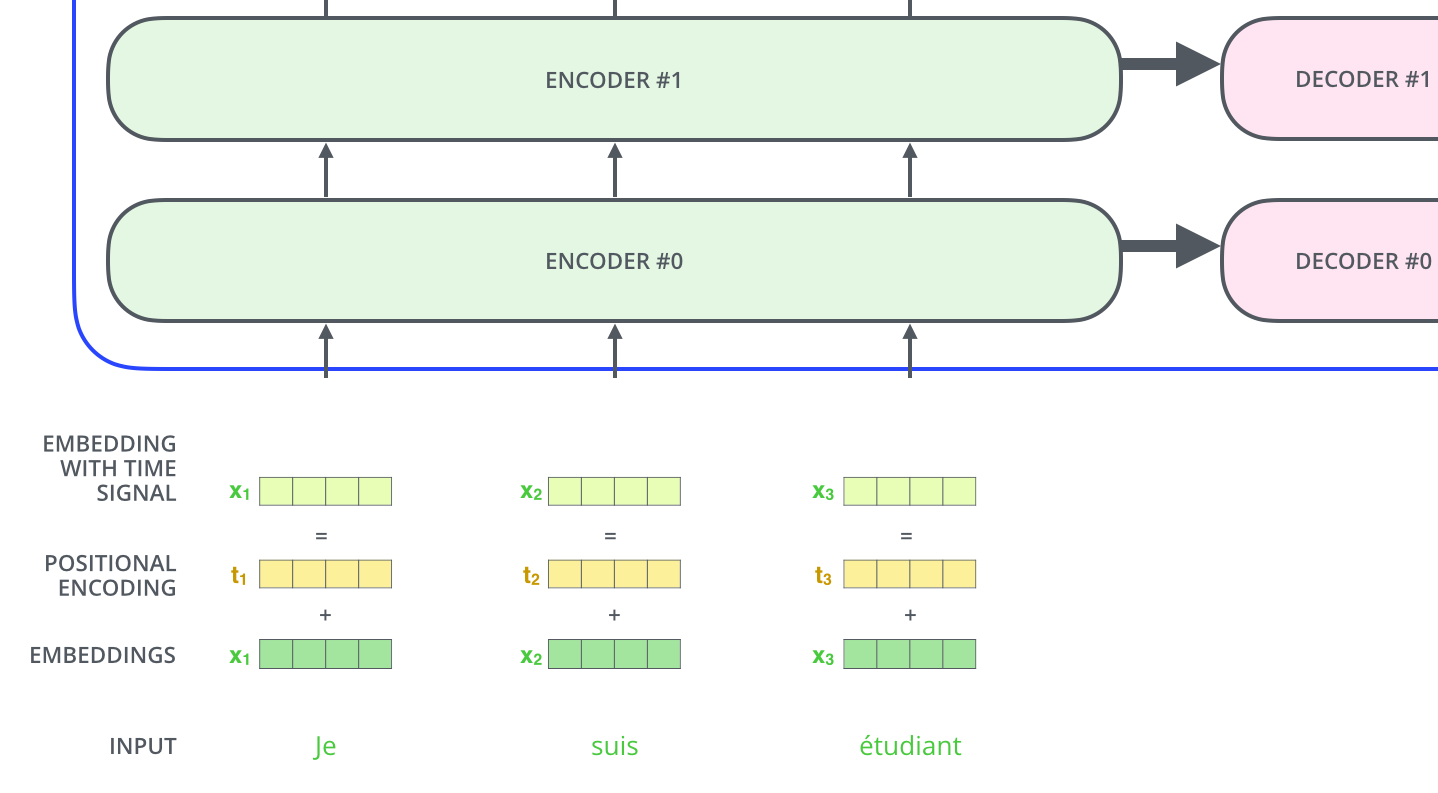Pour donner au modèle un sens de l’ordre des mots, on rajoute des vecteurs d’encodage positionnel – les valeurs desquels suivent un motif spécifique.

Si l’on suppose que l’embedding a une dimensionalité de 4, les vrais encodages positionnels ressembleraient à ça:

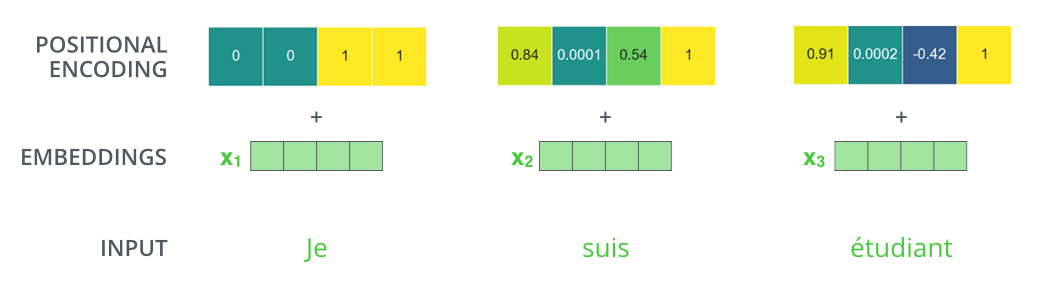Un vrai exemple de l’encodage positionnel, avec un taille d’embedding “jouet” de 4.

Ce motif ressemblerait-il à quoi?

Dans la figure suivante, chaque rangée correspond à l’encodage positionnel d’un vecteur. La première rangée serait le vecteur que l’on ajouterait à l’embedding du chaque mot dans la phrase d’entrée. Chaque rangée contient 512 valeurs – chacun entre 1 et -1. On les montre en code couleur pour que le motif se voie.

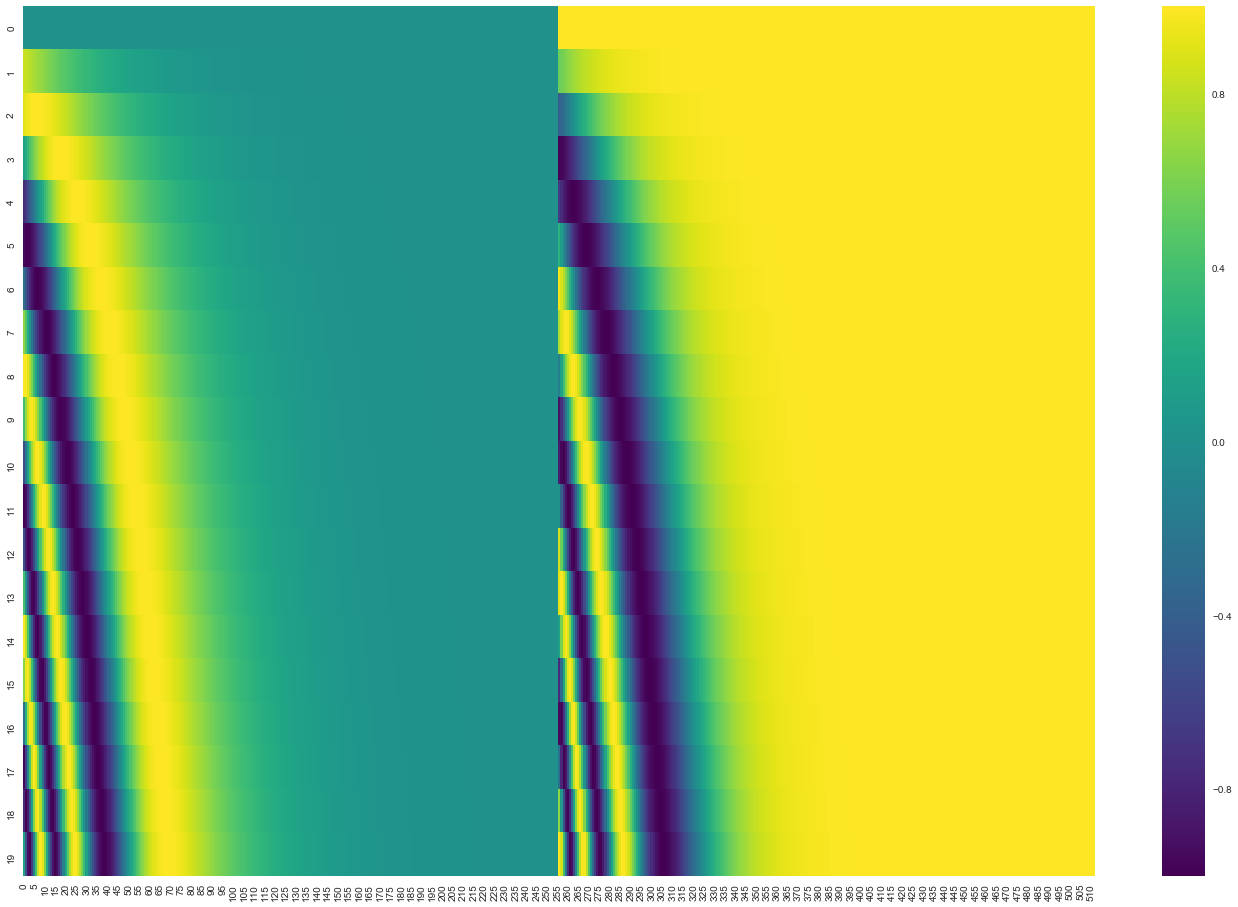Un vrai exemple d’encodage positionnel pour 20 mots (rangées) avec une taille d’embedding de 512 (colonnes). On peut voir que la figure parait être divisé verticalement au centre. C’est parce que les valeurs de la moitié gauche sont générées par une fonction (qui utilise un sinus), et la moitié droite est générée par une autre fonction (qui utilise un cosinus). Elles sont ensuite concatenées pour formuler les vecteurs d’encodage positionnel.

La formule pour l’encodage positionnel se décrit dans l’article (section 3.5). On peut voir le code pour la génération des encodages positionnels en get_timing_signal_1d(). Il n’est pas la seule méthode possible pour l’encodage positionnel. Pourtant, il a l’avantage d’être capable à étendre aux longeurs inconnues de séquence (e.g. si l’on demande à notre modèle entraîné de traduire une phrase plus longue que ce qu’il a vu dans l’entraînement).

Mise à jour de juillet 2020: L’encodage positionnel en haut vient de l’implémentation Transformer2Transformer du transformer. La méthode de l’article est en fait légèrement différent: il ne concatene pas directement; il interfolie plutôt les deux signaux. La figure suivante montre à quoi ça ressemble. Voilà le code pour la générer.

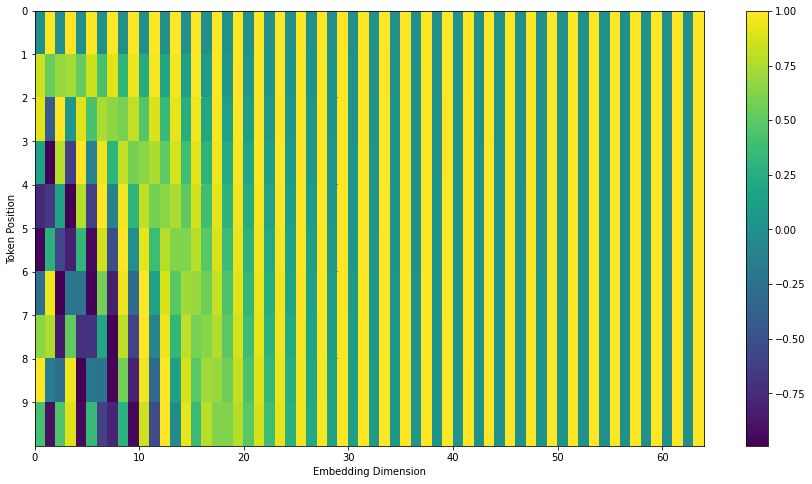
Les résiduels

Un détail dans l’architecture de l’encodeur qu’il faut mentionner avant de continuer, c’est que chaque sous-couche (la self-attention et le feed-forward) dans chaque encodeur a une connexion résiduelle qui l’entoure, suivi par une étape de layer-normalization.

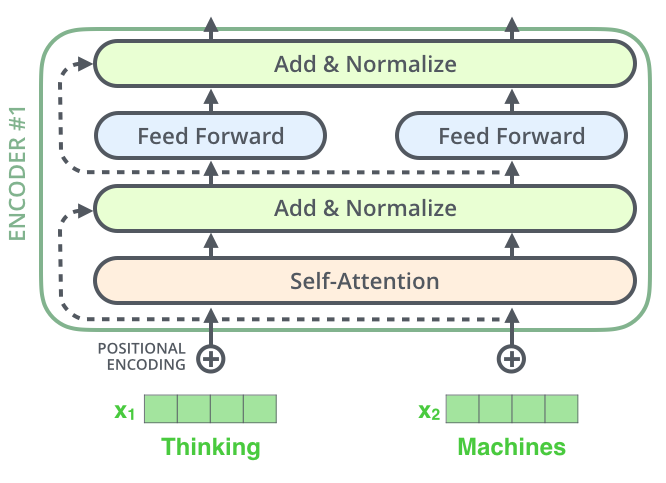
Si l’on visualise les vecteurs et l’operation layer-norm qui s’associe avec la self-attention, il ressemblerait à ça:

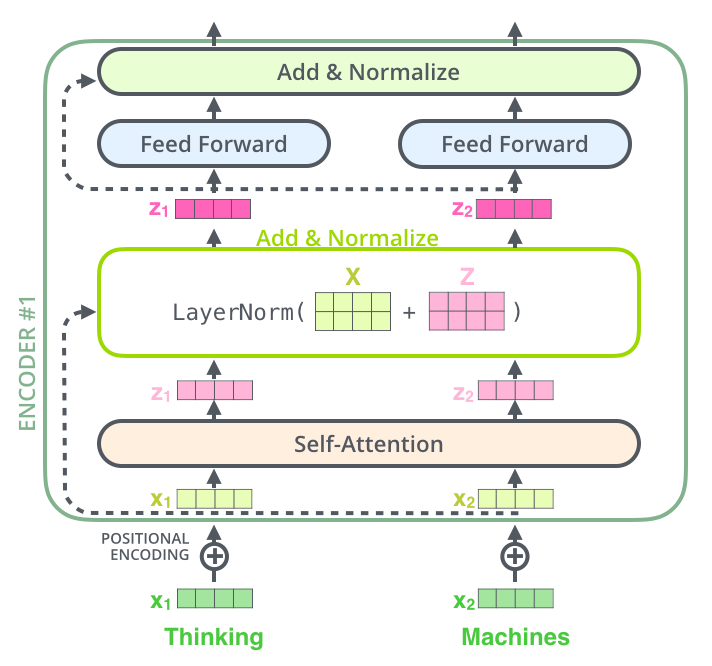
Ceci est vrai aussi pour les sous-couches du décodeur. Si l’on envisage un transformer avec deux encodeurs et décodeurs empilés, il ressemblerait à ça:

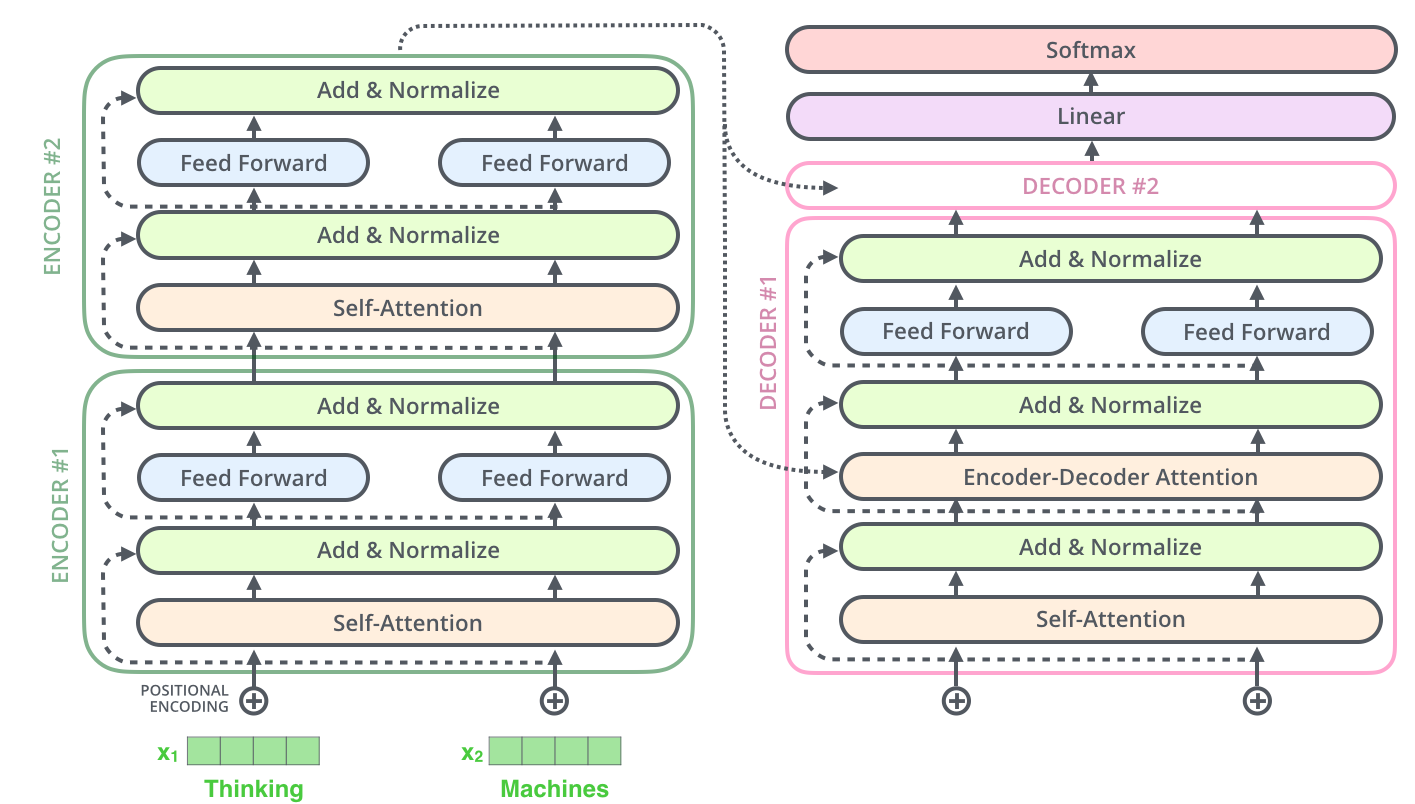
Le côté décodeur

Maintenant que l’on a expliqué la plupart des concepts sur le côte encodeur, on sait plus ou moins comment les composants du décodeur fonctionnent aussi. Mais regardons comment ils fonctionnent tous ensemble.

L’encodeur commence par le traitement de la séquence d’entrée. Les données de sortie de l’encodeur le plus haut se transforme ensuite en les vecteurs d’attention $K$ et $V$. Ces vecteurs seront utilisés par chaque décodeur dans sa couche d’attention encodeur-décodeur, ce qui aide le décodeur à se concentrer sur les positions appropriées dans la séquence d’entrée.

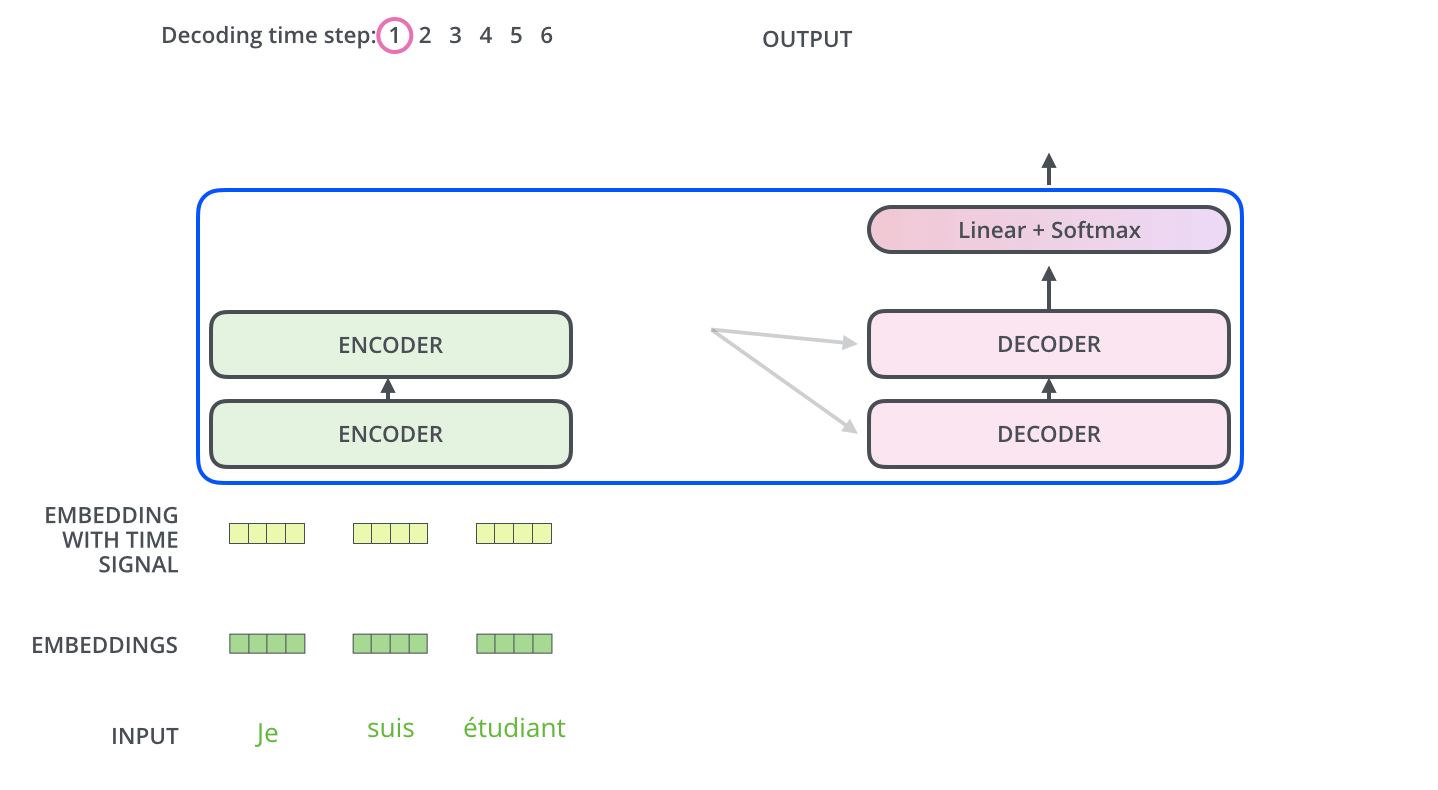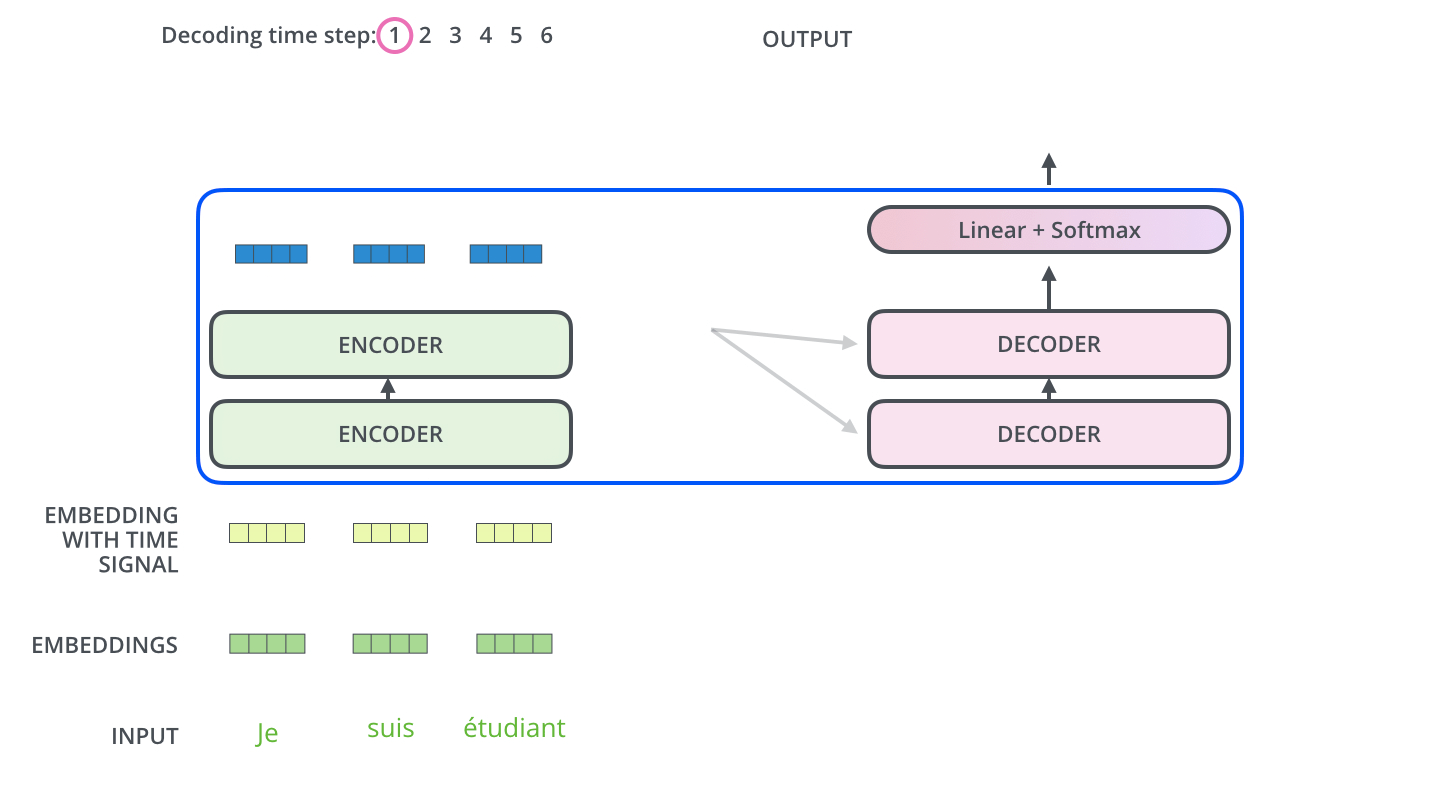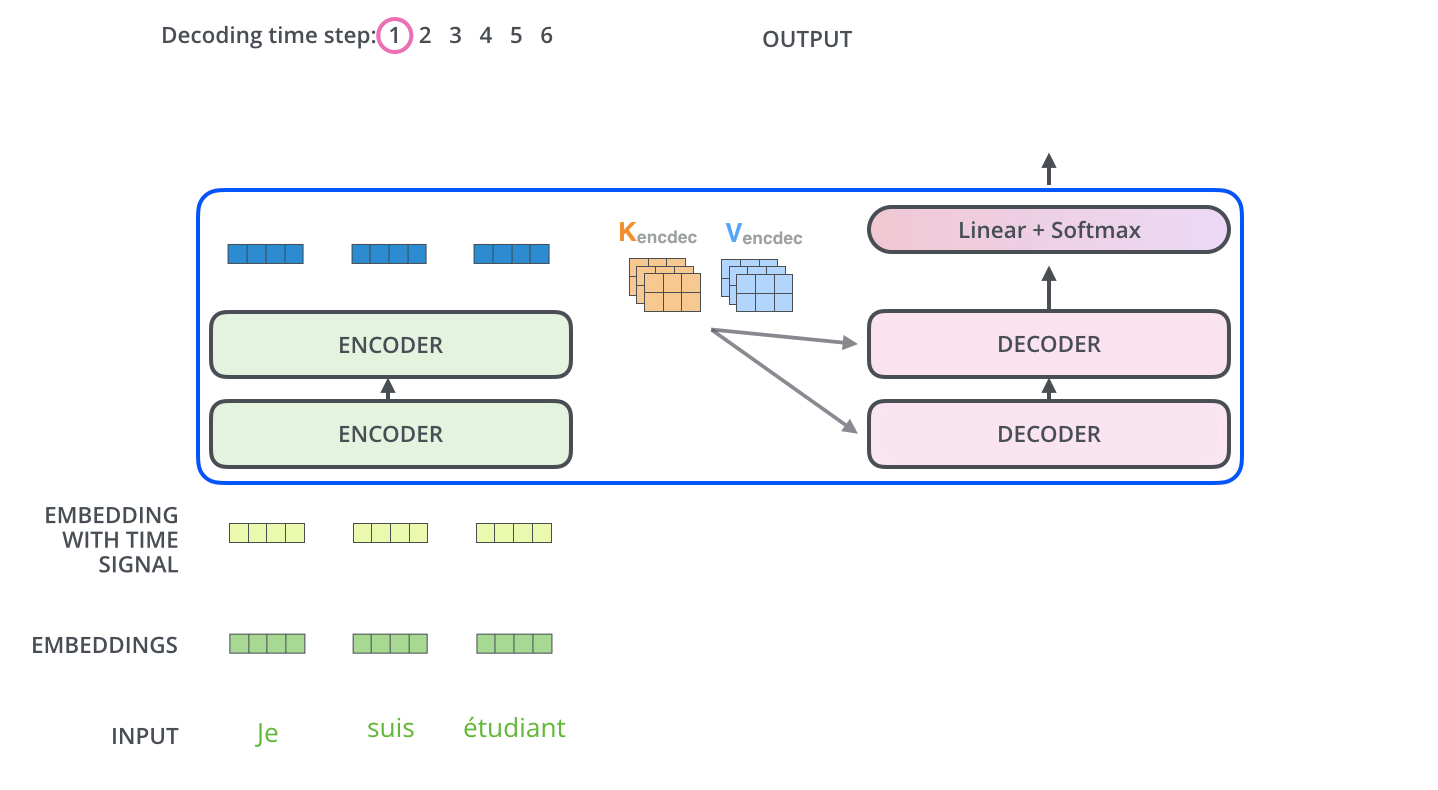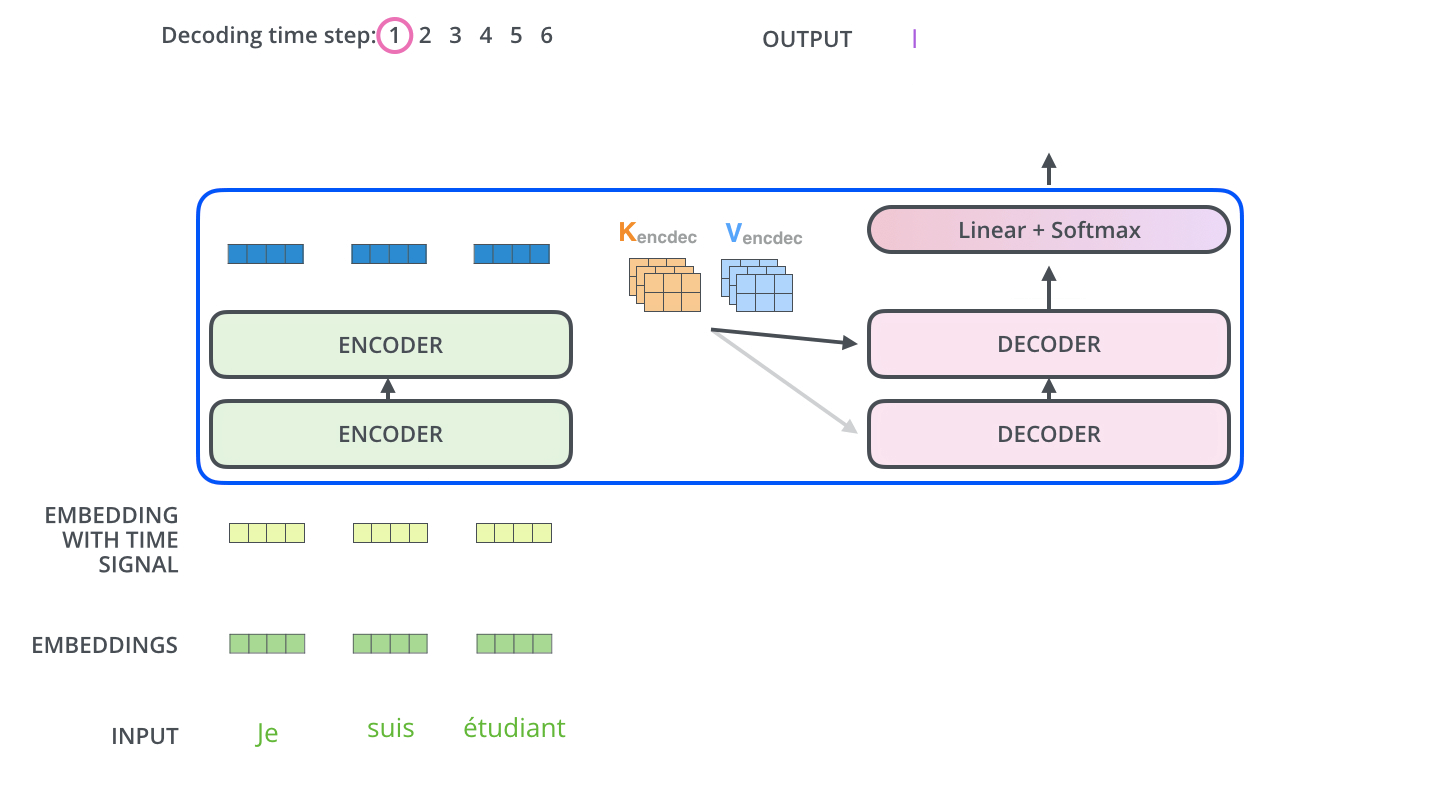Après la phase d’encodage, on commence la phase de décodage. Chaque étape dans la phase de décodage sort un élément de la séquence de sortie (en ce cas, la traduction en anglais).

Les étapes suivantes répètent ce processus jusqu’à ce qu’un symbole spécial s’atteigne, qui indique que le décodeur du transformer a fini. Les données de sortie de chaque étape sont passées au décodeur en bas à la prochaine étape dans le temps, et les décodeurs donnent leur resultats exactement comme les encodeurs. Et comme on a fait avec nos entrées à l’encodeur, on fait un embedding et on rajoute de l’encodage positionnel à ces entrées au décodeur, pour indiquer la position de chaque mot.

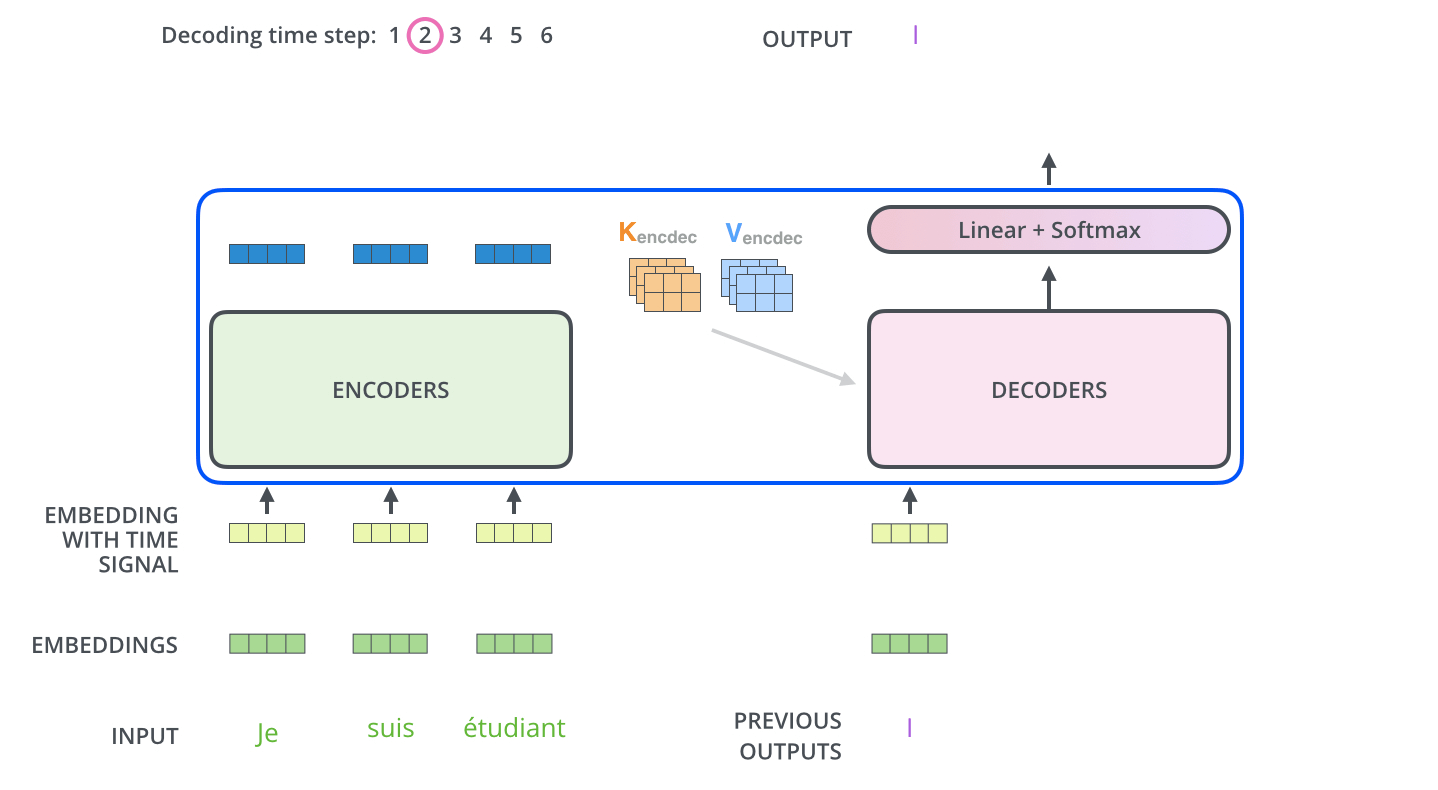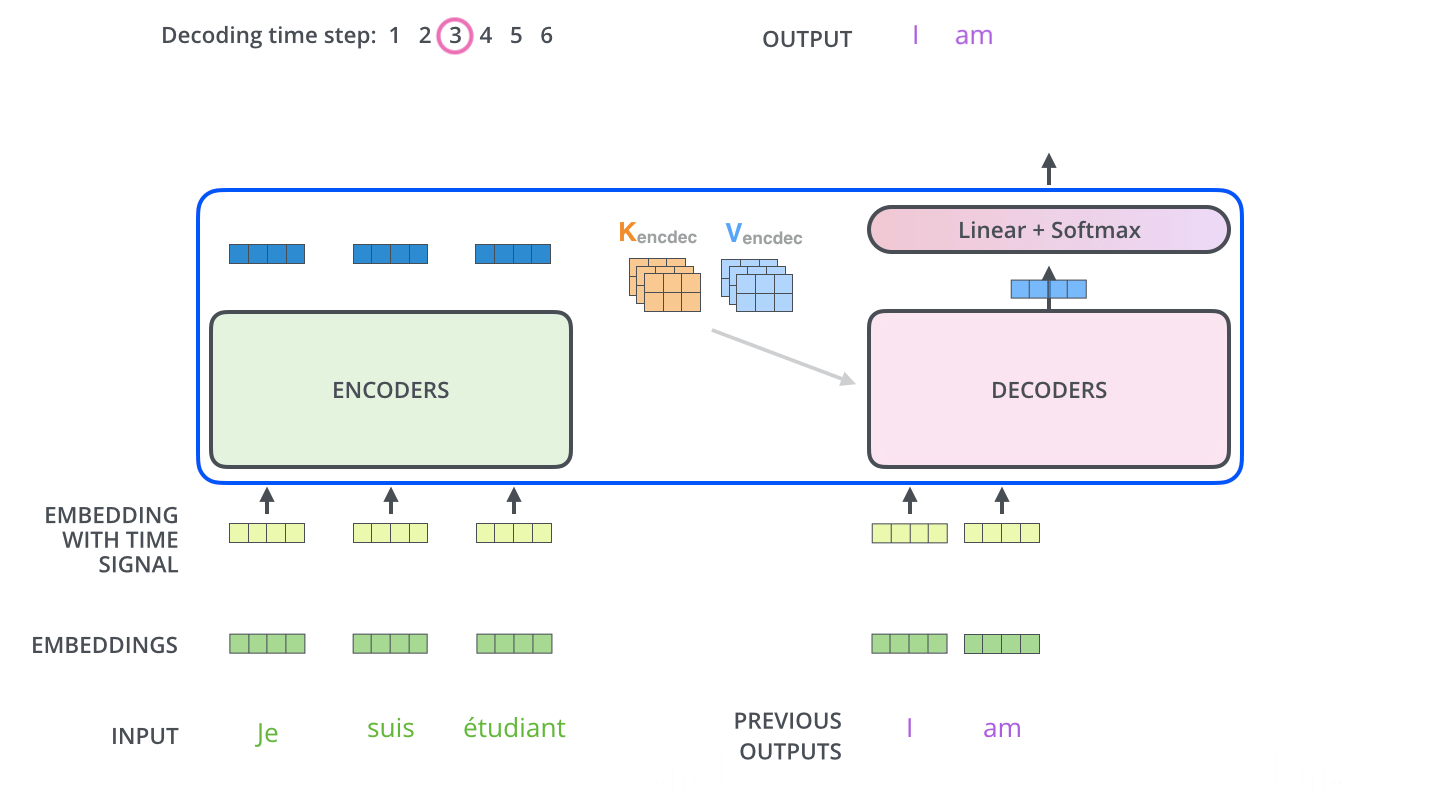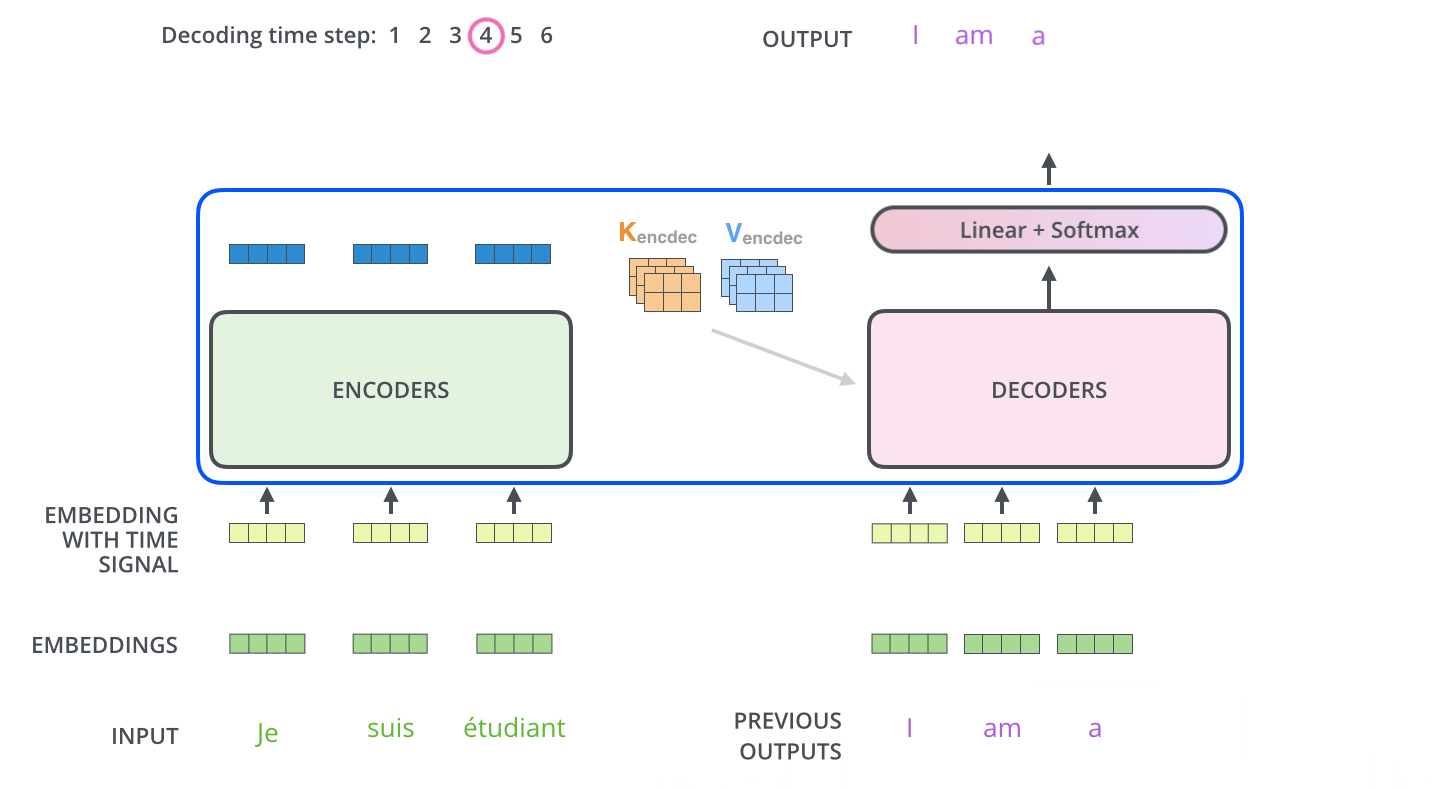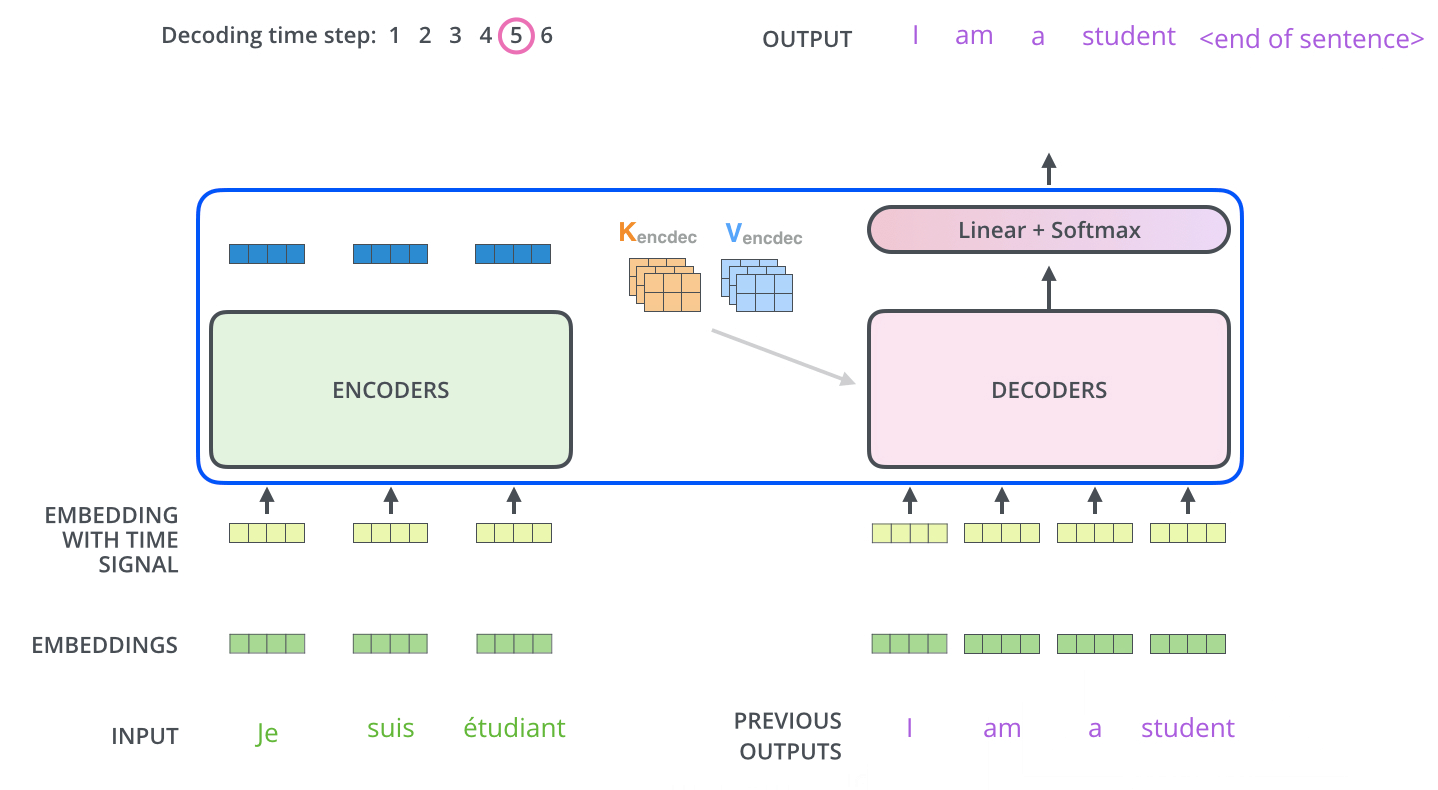
Les couches de self-attention dans le décodeur s’opèrent de manière légèrement différente que celles dans l’encodeur:

Dans le décodeur, la couche de self-attention a le droit à faire attention seulement aux positions plus tôts dans la séquence de sortie. On fait ça en masquant les positions futures (en les mettant a -inf) avant l’étape softmax dans le calcul de la self-attention.

La couche d’attention encodeur-décodeur fonctionne exactement comme la self-attention aux multiples têtes, sauf qu’il crée sa matrice Query de la couche en bas, et il prend les matrices Key et Value de la sortie de la pile d’encodeur.

La couche finale (linéaire et softmax)

La pile de décodeur donne un vecteur de flottants comme sortie. Comment transforme-t-on cela en mot? C’est la tâche de la couche finale lineare, qui se suit par une couche softmax.

La couche linéare est un réseau fully-connected simple qui projette le vecteur donné par la pile de décodeur dans un vecteur beaucoup plus grand qui s’appelle un vecteur de logits.

Supposons que notre modèle connaît 10,000 mots uniques en anglais (le “vocabulaire de sortie” de notre modèle) qu’il a appris de ses données d’entraînement. Ceci donnerait un vecteur de logits de taille 10,000 – chaque cellule correspond au score d’un mot unique. C’est ainsi que l’on interprète la sortie du modèle suivie par la couche linéaire.

La couche softmax transforme ensuite les scores en probabilités (des numéros positifs qui somment à 1.0). La cellule avec la probabilité la plus haute est choisie, et le mot qui y est associé est produit comme la sortie pour cette étape dans le temps).

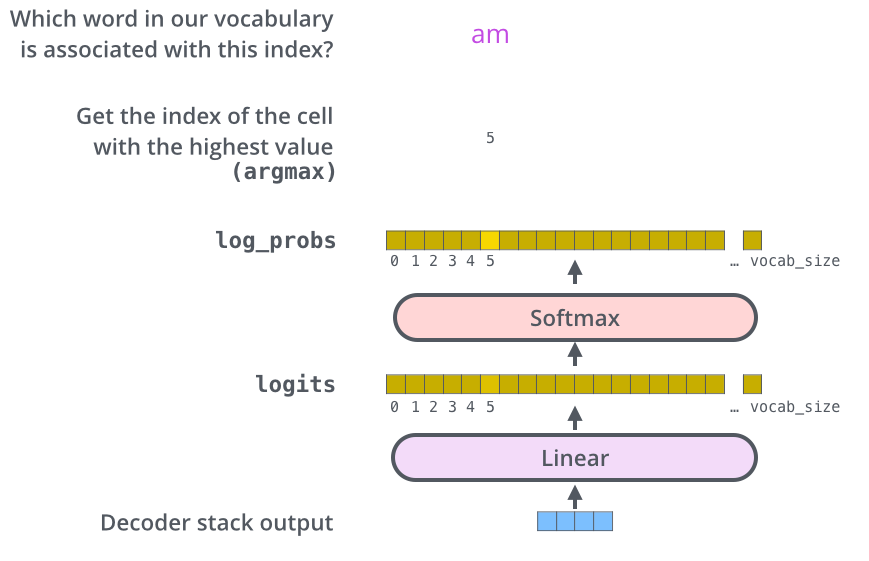Cette figure commence d’en bas, avec le vecteur produit comme la sortie de la pile de décodeur. Il se transforme ensuite en mot de sortie.

Résumé de l’entraînement

Maintenant que l’on a expliqué le processus entier du forward pass d’un transformer entraîné, il serait utile de voir l’intuition de l’entraînement du modèle.

Pendant l’entraînement, un modèle non-entraîné ferait exactement le même forward pass. Mais vu que l’on l’entraîne sur des données étiquettées, on peut comparer ses sorties avec les vraies sorties correctes.

Pour visualiser cela, supposons que notre vocabulaire de sortie ne contient que six mots (a, am, I, thanks, student, et <eos> pour end of sentence, la fin de la phrase).

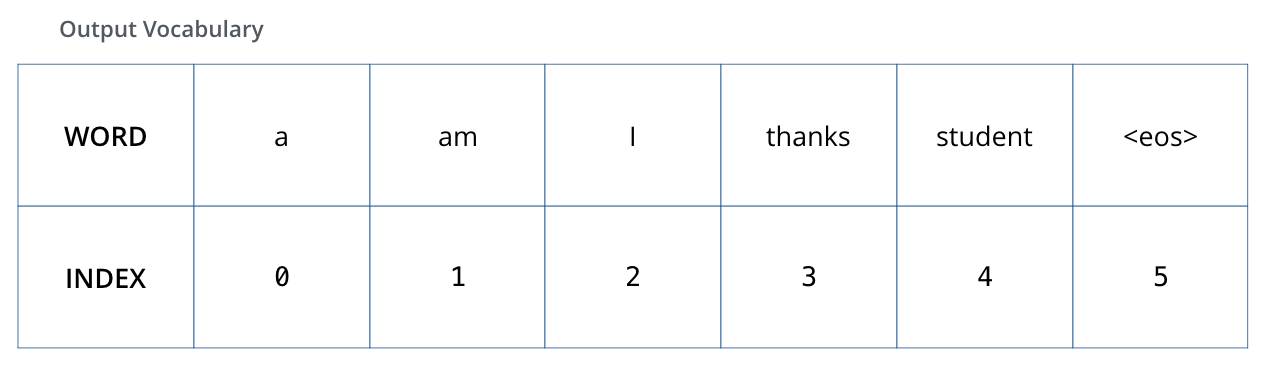Le vocabulaire de sortie de notre modèle se crée pendant la phase preprocessing, avant que l’on commence l’entraînement.

Une fois que l’on défine notre vocabulaire de sortie, on peut utiliser un vecteur de la même longeur pour indiquer chaque mot dans notre vocabulaire. On appelle ça du one-hot encoding. Par exemple, on peut indiquer le mot am avec le vecteur suivant:

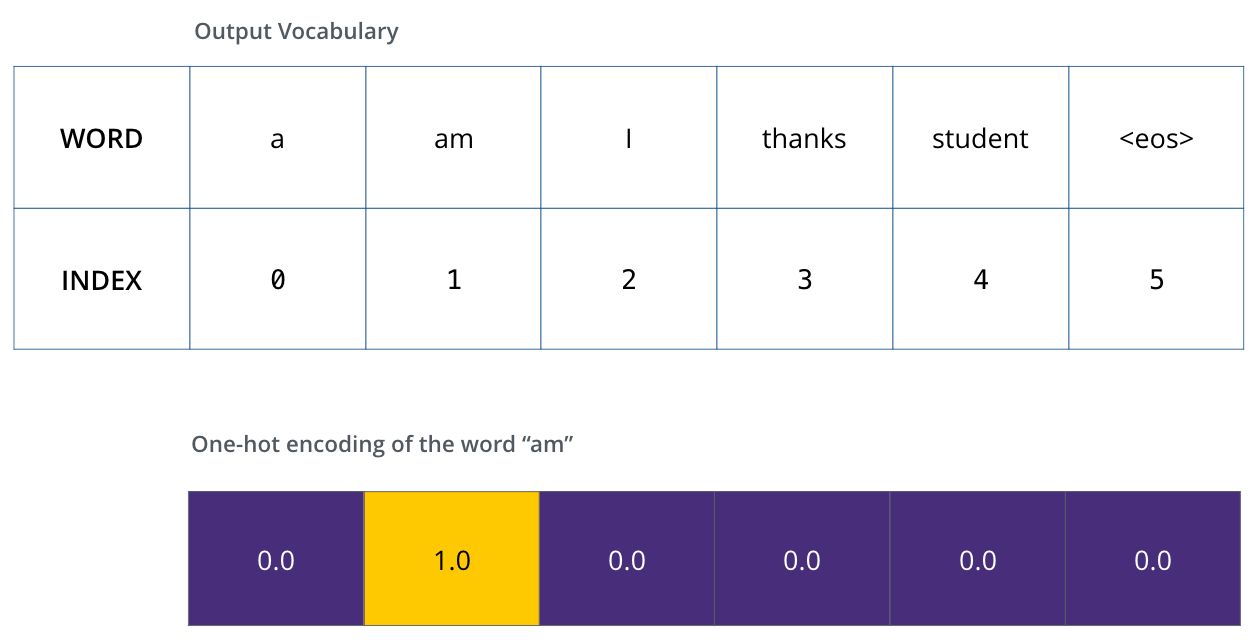Exemple: un one-hot encoding de notre vocabulaire de sortie.

Suivant ce résumé, discutons la fonction de perte de ce modèle – le mesure que l’on optimise pendant la phase d’entraînement pour donner un modèle entraîné et, avec un peu de chance, très juste.

La fonction de perte

Disons que l’on entraîne notre modèle. Disons que c’est la première étape dans la phase d’entraînement, et que l’on l’entraine sur un exemple simple – on va traduire merci en thanks.

Ce que ça veut dire, c’est que l’on voudrait que la sortie soit une distribution de probabilité qui indique le mot thanks. Mais vu que ce modèle n’est pas encore entraîné, il est peu probable que ça arrive maintenant.

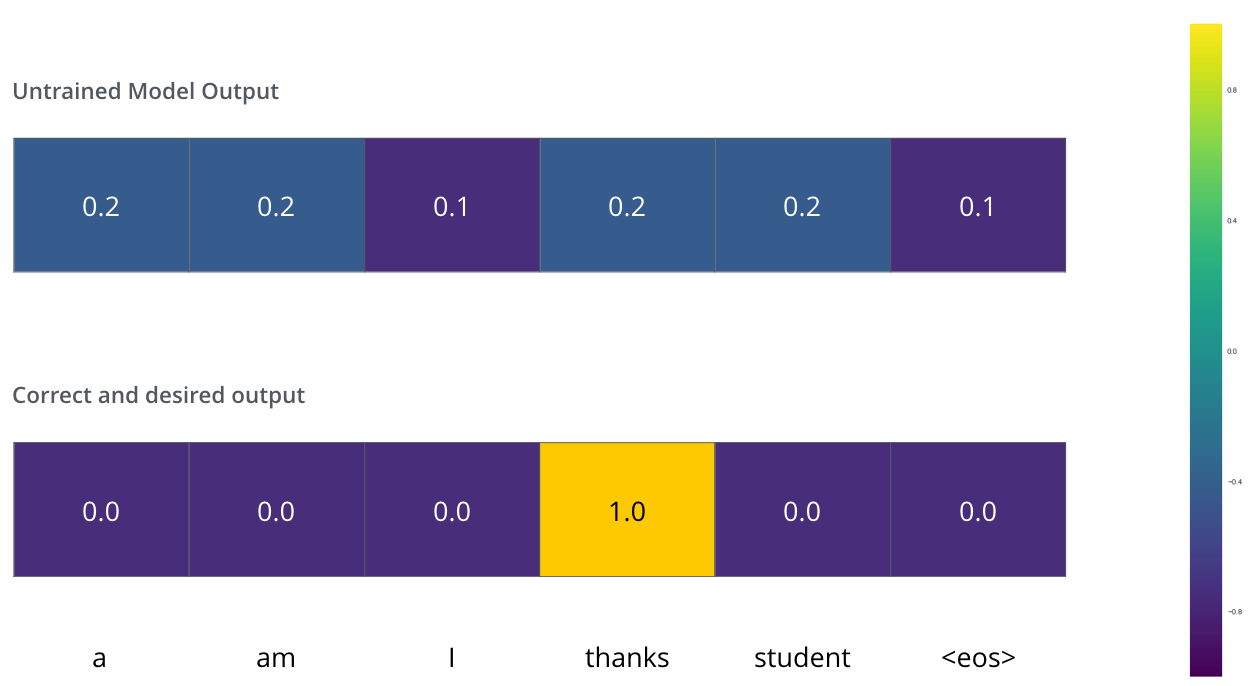Puisque les paramètres du modèle (ses poids) sont tous initialisés de manière aléatoire, le modèle (non-entraîné) produit une distribution de probabilité avec des valeurs arbitraires pour chaque cellule/mot. On peut comparer ça avec la vraie sortie, puis adjuster tous les poids du modèle avec la backpropagation pour rendre la sortie plus proche à la sortie désirée.

Comment peut-on comparer deux distributions de probabilité? Tout simplement, on soustrait l’une de l’autre. Pour plus de détails, voir la cross-entropy et le Kullback-Leibler divergence.

Mais notons que c’est un exemple sur-simplifié. De manière plus réaliste, on va utiliser une phrase plus longue qu’un seul mot. Par exemple, une entrée de je suis étudiant et sa sortie attendue, I am a student. Ce que ça veut dire vraiment, c’est que l’on veut que notre modèle produise en séquence des distributions de probabilité où:

Chaque distribtion de probabilité se représente par un vecteur de longeur vocab_size (6 dans notre exemple jouet, mais de manière plus réaliste, un chiffre comme 30,000 ou 50,000)
La première distribution de probabilité a la probabilité la plus haut à la cellule associée au le mot I
La deuxième distribution a la probabilité a la probabilité la plus haut à la cellule associé au mot am
Et cetera, jusqu’à ce que la cinquième distribution de probabilité indique le symbole <eos>, qui a aussi une cellule associée du vocabulaire de 10,000 éléments.

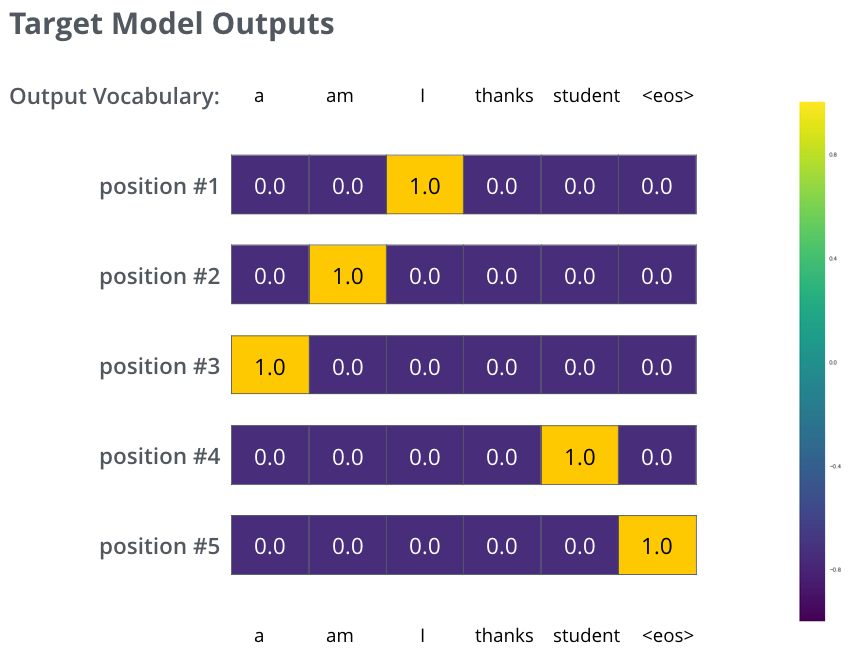Les distributions de probabilité ciblées, contre lesquelles on va entraîner notre modèle.

Après avoir entraîné le modèle pour assez de temps sur assez de données, on aimerait que les distributions de probabilité produites ressembleraient à ça:

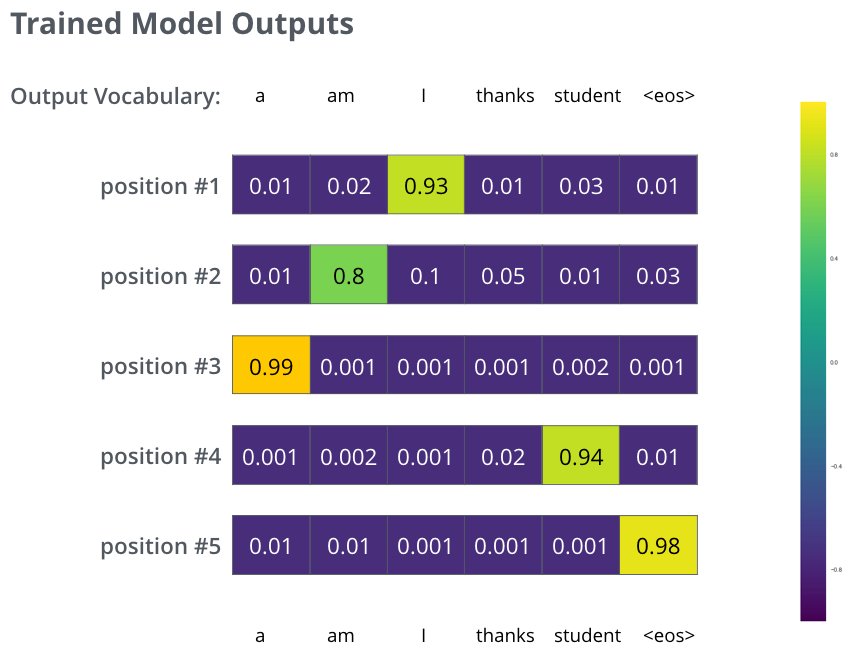On espère que après l’entraînement, le modèle donnerait la bonne traduction. Bien sûr, ce n’est pas une indice fiable si cette phrase faisait partie des données d’entraînement (voir: la cross-validation). Notons que chaque position reçoit un peu de probabilité, même s’il est peu probable que ça soit la sortie de cette étape dans le temps – ceci est une propriété du softmax très utile pour le processus d’entraînement.

Or, parce que le modèle produit les sorties une à la fois, on peut supposer que le modèle sélectionne le mot avec la probabilité la plus haute de cette distribution de probabilité, et qu’il jète le reste. C’est une stratégie possible (qui s’appelle le greedy decoding, un décodage glouton). Une autre stratégie serait de garder, disons, les deux mots les plus probables (I et a, par exemple). Puis dans la prochaine étape, on roulerait le modèle deux fois: une fois en supposant que la première sortie était I, et une autre fois en supposant que la première sortie était a, et on garde la version qui a produit moins d’erreur en considérant les deux positions. On répète ça pour la deuxième et troisième position, etc. Cette méthode s’appelle un beam-search, où dans notre exemple, beam_size était deux (qui veut dire que en tout temps, deux hypothèses partielles, qui sont des traductions non-finies, sont gardées en mémoire), et top_beams est deux aussi (qui veut dire que l’on va retourner deux traductions). Ces deux sont des hyperparamètres que l’on peut adjuster.

Allez et transformez

J’espère que vous ayez trouvé cet article utile pour commencer à comprendre les concepts majeurs du transformer. Si vous voulez en aller plus profondément, je suggère ces étapes suivantes:

Lire l’article Attention is All You Need, le blog post sur le transformer (Transformer: A Novel Neural Network Architecture for Language Understanding), et l’annonce Tensor2Tensor.
Regarder la présentation de Łukasz Kaiser qui montre les détails du modèle
Jouer avec le notebook Jupyter fourni avec Tensor2Tensor
Explorer Tensor2Tensor.

Des œuvres suivants:

Remerciments

Merci à Illia Polosukhin, Jakob Uszkoreit, Llion Jones, Lukasz Kaiser, Niki Parmar, and Noam Shazeer pour avoir donné du feedback sur les versions initiales de cet article.

Vous pouvez contacter l’auteur sur Twitter avec des corrections ou du feedback.

PREVIOUSBERT, ELMo, et cie, illustrés (Comment NLP a percé le mystère du transfer learning)

NEXTVisualizing Barth: Two Planes